Доброго времени суток!
Как я поняла, вопрос был поставлен таков : "Стороны равнобедренного треугольника пропорциональны числам 1, 1, √2. Докажите, что этот треугольник — прямоугольный".
если это не так, то сообщите об этом в комментариях.
▔ ▔ ▔
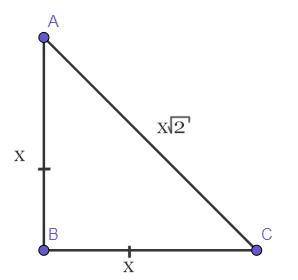
★☆★ Чертёж смотрите во вложении ★☆★
Дано:ΔАВС — равнобедренный (АВ = ВС).
АВ : ВС : АС = 1 : 1 : √2.
Доказать:ΔАВС — прямоугольный.
Доказательство:▸Теорема, обратная теореме Пифагора — если квадрат большей стороны треугольника равен сумме квадратов других сторон, то такой треугольник — прямоугольный◂
Итак, пусть АВ = ВС = х, тогда, по условию задачи, АС = х√2.
Составим уравнение и проверим его на верность —
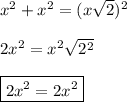
Итак, мы выяснили, что сумма квадратов меньших сторон равна квадрату большей стороны. Поэтому, по обратной теореме Пифагора, равнобедренный ΔАВС — прямоугольный.
ответ:что требовалось доказать.
Теперь надо построить хорду C1D1, симметричную CD относительно OY; ясно, что она параллельна CD и перпендикулярна AB, ясно, что C1D1 = CD; и вообще - CDD1C1 это прямоугольник. Что означает, что CD1 - диаметр.
Поскольку при зеркальном отражении относительно OY точка A переходит в B, а точка D - в точку D1, то BD = AD1; (по определению равенства фигур, между прочим).
Остается заметить, что, раз CD1 - диаметр, то треугольник ACD1 - прямоугольный, и записать для него теорему Пифагора.