ответ: 1200π
Объяснение:
Формула объёма прямой призмы V=S•H, где Ѕ - площадь основания, Н - высота призмы.
Высота призмы равна высоте вписанного цилиндра, которая, в свою очередь, равна его оси. Ось цилиндра параллельна боковой грани призмы, диагональ боковой грани принадлежит её плоскости. Эти два отрезка не пересекаются и не параллельны - они скрещиваются. Расстоянием между скрещивающимися прямыми называется расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой.
Окружность основания цилиндра касается боковой грани призмы, радиус перпендикулярен стороне основания, поэтому расстояние между осью цилиндра и диагональю боковой грани призмы равно радиусу цилиндра.
Ѕ(полн. цил)=2Ѕ (осн)+Ѕ(бок).
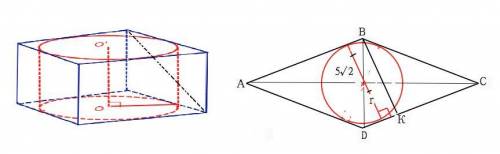
Ѕ(осн)=πr²=π•(5√2)²=50π ⇒2S=100π
Ѕ(бок)=106π-100π=6π
Ѕ(бок)=2πr•H ⇒ H=6π:2π•5√2=0,3√2
Высота ВК основания (ромба) равна диаметру основания цилиндра=2r=10√2
Сторона ромба АВ=ВС=ВК:sin45°=(10√2•√2):2=20
S(ABCD)=AB•AC•BK=200•10√2=2000√2
V=π•2000√2•0,3√2=1200π
Фактически задача сводится к нахождению координат вектора CD.
Мы знаем, что СD перпендикулярно AB. И CD проходит через точку C.
Условие перпендикулярности -> косинус угла между векторами CD и AB равен нулю.
Формула косинуса угла между векторами - 
AB={-1+5;4-1}={4;3}
CD={x2-3;y2-2}
Составим уравнение прямой АВ: 
(*)
Подставляя вместо x1 и y1 в формулу косинуса 4 и 3 соответственно получим:
4(x2-3)+3(y2-2)=0
Также точка D принадлежит прямой AB, а значит x2 и y2 удовлетворяют уравнению (*).
Решаем полученную систему уравнений.
Мне лень решать - сами решите. Как найдёте x2 и y2 - подставьте их и найдите координаты вектора CD. Зная координаты направляющего вектора и точку, через которую проходит прямая, легко составить уравнение прямой.
Оно выглядит так: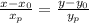 
, где 
- координаты напрвляющего вектора (в нашем случае вектора CD), а х0 и у0 - координаты точки, через которую проходит прямая (в нашем случае С или D - на выбор)
Ну, обычным методом я легко решу.
Надо построить прямую пересечения АВ1D и АВС. В плоскости грани ВВ1С1С продлим прямые ВС (за точку С) и В1D (за точку D) до пересечения - пусть это точка Е. Очевидно, что точка Е принадлежит плоскости АВС. И очевидно, что раз D - середина СС1, то треугольники В1С1D и DCE равны (по стороне и 2 углам). Поэтому DE = B1D, и СЕ = В1С1 = ВС = 2.
Прямая АЕ содержит 2 точки ( А и Е), принадлежащие плоскостям АВС и B1АD, поэтому АЕ - ребро двугранного угла между этими плоскостями. Чтобы вычислить линейный угол двугранного угла, заметими, что угол АСЕ - внешний угол треугольника АВС, поэтому он равен 120 градусам. Получается, что треугольник АСЕ - равнобедренный с боковыми сторонами АС = СЕ = 2 и углом при вершине 120 градусов.
Если через точки D, C и середину АЕ (пусть это точка М) провести плоскость, то СМ перпендикулярна АЕ и DC перпендикулярна АЕ (DC препендикулярна вообще всей плоскости АВС, в том числе и лежащей в ней прямой АЕ). Поэтому плоскость DCM перпендикулярна АЕ, и угол DMC и есть искомый угол. Обозначим его Ф.
При этом СМ - высота к основанию в равнобедренном треугольнике АСЕ. Угол при основании (например, угол САЕ) равен 30 градусов, поэтому СМ = АС/2 = 1;
DC = CC1/2 = 1/2;
tg(Ф) = DC/CM = 1/2;
Координатным тоже можно. Разместим начало координат в точке А. Ось X пустим II BC, ось Y перпендикулярно ВС. Ось Z это АА1. Тогда уравнение плоскости АВС z = 0, и координаты нормального вектора n = (0, 0, 1).
Найдем координаты точек В1 и D. Напомню, что сторона основания равна 2, то есть высота равна корень(3).
Координаты точки С, очевидно, (1, корень(3), 0), точки В (-1, корень(3), 0)
Поэтому B1 (-1, корень(3), 1), D (1, корень(3), 1/2);
Напомню, что точка А (0, 0, 0); составим уравнение плоскости, проходящей через А, В1, D.
Запишем определитель
Ix y z I
I-1 корень(3) 1 I
I1 корень(3) 1/2 I
Или, в обычном виде,
x*(корень(3)*(1/2) - корень(3)*1) - y*((-1)*(1/2) - 1*1) + z*((-1)*корень(3) - 1*корень(3)) = 0;
(корень(3)/2)*x - (3/2)*y + 2*корень(3)*z = 0;
РАзделим на корень(3)/2, получим
x - y*корень(3) + 4*z = 0; (если есть сомнения, непосредственной проверкой убеждаемся, что точки B1 (-1, корень(3), 1), D (1, корень(3), 1/2) принадлежат этой плоскости)
Нормальный вектор p = (1, корень(3), 4)
Найдем его модуль. IpI^2 = 1 + 3 + 16 = 20; IpI = 2*корень(5);
Угол между плоскостями равен углу между нормальными векторами, то есть
cos(Ф) = np/IpI = 4/(2*корень(5)) = 2*корень(5)/5.