Объяснение:
Все задачи решаются через площади треугольников: S(△)=1/2*a*h; S=√p(p-a)(p-b)(p-c); и параллелограмма: S(пар)=a*h
1) S=1/2*16*12=96; с - гипотенуза, с=√(16²+12²)=√(256+144)=20
S=1/2*c*h; h=96*2/20=9.6
2) Если принять, что там дан параллелограмм (в условии этого не сказано, но по-другому я не знаю как решить), то
S(пар)=2*3=6 (через сторону равную 3 и высоту равную 2)
S(пар)=5*h (через другую сторону и искомую высоту) => h=6/5=1.2
3) p=(a+b+c)/2=34
S=√34(34-17)(34-25)(34-26)=√34*17*9*8=204
S=1/2*26*h; h=2*204/26=204/13=15 9/13 (примерно 15,69)
4) a - катет, а=√(25²-20²)=15
S=1/2*15*20=150
S=1/2*25*h; h=2*150/25=12
1. вектор AB + вектор BD= вектор AC + вектор CD
2. вектор AB + вектор BC= вектор AD + вектор DC
Это правило треугольника сложения векторов: Видим что конец первого вектора совпадает с началом второго. Значит результатом сложения будет вектор, обозначенный первой буквой первого вектора и второй буквой другого вектора:
АВ + ВD = AD, AC + CD = AD
Видим, что результаты сложения совпадают, что и требовалось доказать.
Аналогично и во втором примере:
AB + BC = AC, AD + DC = АС, что и треб. доказать.
АВСD - параллелограмм
1. CA = СВ + ВА = CD + DA
2. DA = DC + CA = DB + BA
1. вектор AB + вектор BC = AC
2. вектор MN + вектор NN = MN
3. вектор PQ+ вектор QR = PR
4.вектор EF + вектор DE = DE + EF = DF
выразите вектор BC через векторы AB и AC:
BC = AC - AB
взята точка D на стороне треугольника ABC. Выразите вектор BD через векторы AB и AD:
BD = AD - AB
Дан параллелограмм ABCD. Найдите разность:
1. вектор AB- вектор AC = CB
2. вектор BC - вектор CD = AB+BC = AC
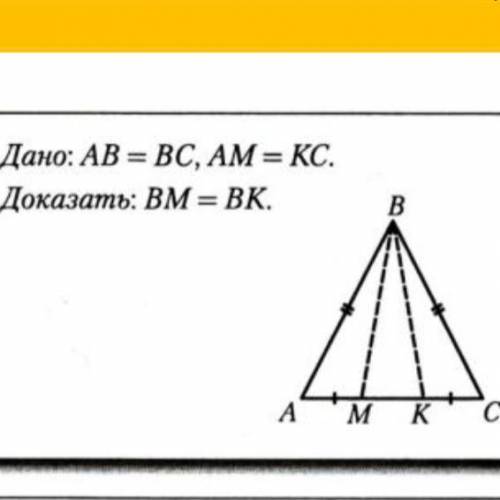
Я буду использовать равенство треугольник.
Треугольник ABM равен треугольник CBK по двум сторонам AB=BC и AM=KC ( по условию) и углу прилежащиму между ними, угол ABM равен углу СBK, следовательно треугольник ABM равен треугольнику СBK.
Из равенства треугольников следует, что BM=BK, что и требовалось доказать