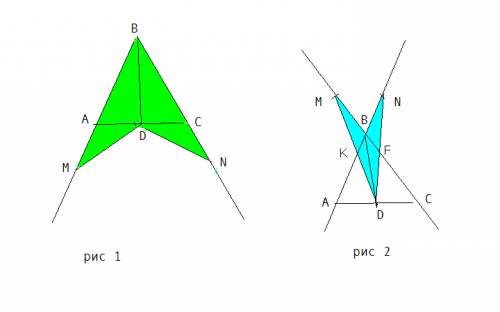
Данная задача может быть представлена в двух случаях ( см рисунок)
По первому рисунку доказательство Так как треугольник АВС равнобедренный, то медиана ВД также является биссектриссой и высотой, следовательно угол АВД=углу СВД.
ΔВДМ=ΔBDN( по первому признаку равенства теугольников: BM=BN ( по условию); BD- общая;угол АВД=углу СВД из доказанного выше)
По второму рисунку <MBK=<NBF как вертикальные, <KBD=<FBD, так как BD биссектрисса равнобедренного треугольника) Сумма двух равных углов равна. Поэтому
ΔВДМ=ΔBDN( по первому признаку равенства теугольников: BM=BN ( по условию); BD- общая;<MBD=<NBD из доказанного выше)
216см2
Объяснение:
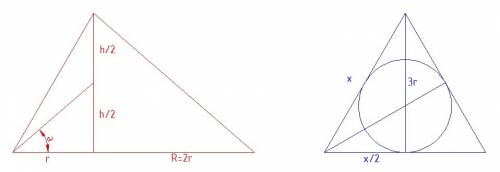
Центр окружности, описанной около равнобедренной трапеции, который находится на большем основании, делит его на две равные части:
AO=OD=R=1/2×AD=1/2×26=13 см
2. В равнобедренной трапеции AE и FD можно найти, зная основания:
AE=FD=(AD−BC)/2=(26-10)/2=8
Вычисляем EO и OF:
EO=OF=R−AE=13−8=5 см
3. Так как ΔEBO — прямоугольный, то высоту трапеции BE можно найти по теореме Пифагора:
BE=R2−EO2−−−−−−−−√=132−52−−−−−−−√=169−25−−−−−−−√=144−−√=12 см
4. Вычисляем площадь трапеции:
S=AD+BC2×BE=(26+10)/2×12=18×12=216см2
1)рассмотрю эти треугольники.
1)BM = BN - по условию
2)BD - общая
3)<NBD = <MBD - так как NBA = <MBC, как вертикальные, а <ABD = <CBD, по св. медианы в равноберенном треугольнике, проведённой к основанию
Отсюда делаем вывод, что данные треугольники равны по двум сторонам и углу между ними. Всё )