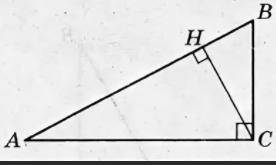
Обозначим прямоугольник АВСД. Диагональ АС. На неё из вершины В опущен перпендикуляр ВК, и по условию АК=9, КС=16. ВК это общая высота в прямоугольных треугольниках АВК и СВК. Отсюда по теореме Пифагора АВ квадрат-АК квадрат=ВС квадрат-КС квадрат. Или АВ квадрат-81=ВС квадрат-256. Отсюда ВС квадрат=АВ квадрат+175. В треугольнике АВС также АВ квадрат+ ВС квадрат= АС квадрат. Или АВ квадрат+ВС квадрат=(9+16)квадрат. АВ квадрат+ ВС квадрат=625. Подставим сюда ранее найденное выражение для ВС квадрат и получим АВ квадрат+(АВ квадрат+175)=625. Отсюда АВ=15. ВК=корень из(АВ квадрат-АК квадрат)=корень из(225-81)=12. Искомый тангенс угла ВАК, tg=ВК/АК=12/9=4/3.
Получилось как-то многословно, но, надеюсь, понятно)
Продолжим прямые, соединяющие середину боковой стороны с двумя вершинами, до пересечения с продолжениями сторон.
Из равенства прямоугольных треугольников (прямой угол, равное расстояние от оснований трапеции и вертикальный угол) будет следовать тот факт, что точка пересечения диагоналей новой фигуры делит эти диагонали пополам.
Следовательно, мы построили параллелограмм (это его свойство). По рисунку так же понятно, что диагонали нашего параллелограмма будут равны друг другу. Но из всех видов параллелограмма лишь у прямоугольника диагонали могут быть равны друг другу, следовательно, на самом деле мы построили прямоугольник. Ну а раз у нашей новой фигуры все углы прямые, то и у трапеции 2 левых угла равны 90°, что и говорит о её прямоугольности.