Понятно, зачем нам сказано, что биссектрисы пересекаются в одной точке - ведь эта точка равноудалена от . сторон четырехугольника и поэтому является центром вписанной окружности. А раз в четырехугольник можно вписать окружность, суммы противоположных сторон равны. Таким образом, ME+BD=MD+BE. Это равенство позволяет найти третью сторону треугольника, используя связь между сторонами и медианами треугольника, а также тот факт, что медианы в точке пересечения делятся в отношении 2:1, считая от вершины.
Пусть AB=c, BC=a, CA=b, тогда
 . Поэтому
. Поэтому
 а умножив для упрощения это равенство на 6 и подставив b=12 и c=10, получаем
а умножив для упрощения это равенство на 6 и подставив b=12 и c=10, получаем
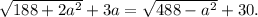
При всей моей любви к иррациональным уравнениям, решать это уравнение не хочется. Давайте попробуем угадать решение. И если Вы достаточно настойчивы, то удача в этой задаче к Вам придет - подходит a=10. ( ). Другого решения быть не может, поскольку при a>0 правая часть возрастает, а левая убывает.
). Другого решения быть не может, поскольку при a>0 правая часть возрастает, а левая убывает.
Таким образом, мы доказали, что наш треугольник равнобедренный со сторонами 12, 10 и 10. Иными словами, он состоит из двух прямоугольных треугольников с гипотенузой 10 и катетом 6, то есть треугольников, подобных египетскому 3-4-5. Площадь египетского треугольника равна 6, подобного треугольника с коэффициентом подобия 2 равна 24, а поскольку их два, суммарная площадь равна 48.
И наконец, кто не знает формулу для длины медианы, можно воспользоваться или теоремой косинусов, или теоремой Стюарта, или теоремой о сумме длин диагоналей параллелограмма.
Объяснение:
Дан правильный тетраэдр EPGS, у которого EF = 12.
Точки L и N лежат на ребрах SG и SE соответственно, причем SL = 3, SN = 3. Точка Т - середина ребра SF.
Найдите:
а) точку Y1 пересечения прямой TL и плоскости EFG;
б) точку Y2 пересечения прямой TN и плоскости EFG;
в) длину отрезка Y1Y2;
г) точку пересечения прямой TN и плоскости ELF;
д) прямую пересечения плоскостей LY1Y2 и NFE;
е) отношение, в котором плоскость LY1Y2 делит отрезок SE, считая от точки S.
Определение: Тетраэдр называется правильным, если все его грани - равносторонние треугольники.
а) точка Y1 должна лежать на линии пересечения плоскостей GSF и EFG, так как прямая TL лежит в плоскости GSF. Для ее нахождения продлим прямую TL за точку Т до пересечения с продолжением прямой GE (линии пересечения плоскостей GSF и EFG.
б) точка Y2 должна лежать на линии пересечения плоскостей ЕSF и EFG, так как прямая TN лежит в плоскости ESF. Для ее нахождения продлим прямую TN за точку Т до пересечения с продолжением прямой EF (линии пересечения плоскостей ESF и EFG.
в) Проведем в грани GSF прямую LH параллельно ребру SF. Треугольник GLH подобен треугольнику GSF, следовательно он правильный и LH = GL = 9 ед. Треугольники LHY1 и TFY1 также подобны с коэффициентом подобия k = TF/LH = 6/9 = 2/3. Тогда FY1/HY1 = 2/3 => FY1/(FY1+HF) = 2/3. HF = 3 (HF=SL, так как LH║SF) => FY1 = 6 ед.
Аналогично и для грани ESF => FY2 = 6 ед.
Треугольник Y1FY2 равнобедренный с углом при вершине F равным 60° (он вертикальный с углом EFG правильного треугольника EFG). Следовательно, это правильный треугольник и его сторона
Y1Y2 = Y1F = Y2F = 6 ед.
г) точка пересечения прямой TN и плоскости ELF - это точка Y2, так как плоскости ELF и ESF пересекаются по прямой EF, следовательно, прямая TN, лежащая в плоскости ESF, пересечет плоскость ELF в точке Y2 на линии пересечения этих плоскостей.
д) прямая пересечения плоскостей LY1Y2 и NFE - это прямая TY2 (NY2), так как точки Т и Y2 принадлежaт плоскости NFE (SEF) и плоскости LY1Y2.
е) точка N принадлежит плоскости LY1Y2, так как эта плоскость определяется как единственная пересекающимися прямыми LY1 и NY2. SN = 3, а SE = 12(дано), значит NE = 12 -3 =9). Следовательно, плоскость LY1Y2 делит отрезок SE в отношении SN/NE = 1:3, считая от точки S.
P.S. Пункт в) можно решить по теореме Менелая.
Для треугольника GSF и секущей LY1 имеем:
(GL/LS)*(ST/TF)*(FY1/Y1G) = 1. Подставим известные значения:
(9/3)*(6/6)*(FY1/Y1G) = 1 => FY1/Y1G = 1/3. Или
FY1/(12+FY1) = 1/3. => FY1 = 6 ед.
Аналогично для треугольника ESF и секущей NY2 получаем
FY2 = 6 ед.