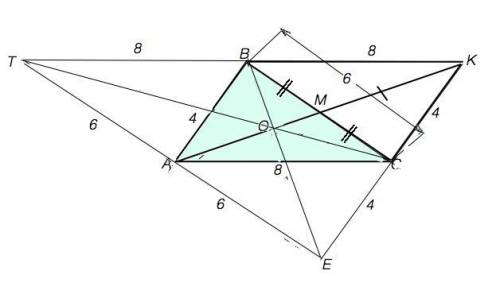
Пусть в треугольнике АВС стороны АВ=4 см, ВС=6 см, АС=8 см. Достроим треугольник АВС до параллелограмма АВКС и проведём диагональ АС. Сторона ВС в этом параллелограмме является второй диагональю. Диагонали пересекаются в точке М, которая делит их пополам. ВМ=СМ и АМ=КМ.
В параллелограмме сумма квадратов всех сторон равна сумме квадратов диагоналей. ⇒ АВ²+ВК²+КС²+АС²=АК²+ВС² ⇒2•(16≠64)=36+АК² ⇒ АК²=124, откуда АК=2√31. Медиана к ВС – половина АК и АМ =√31 см простой, вычисления несложные. Медиану к ВА аналогичным можете найти из параллелограмма АТВС, медиану к АС – из параллелограмма АВСЕ.
Медиану треугольника, стороны которого известны, можно найти и по формуле М=[√(2а*+2b*-с*)]:2, где а и b - стороны, между которыми медиана проходит, с - сторона, к которой медиана проведена.
∠A = 70°, ∠B = 110°, ∠C = 125°, ∠D = 55°.
Объяснение:
Сумма углов, прилегающих к боковой стороне трапеции равна 180° (как внутренние односторонние при параллельных рснованиях и секущей - боковой стороне). Значит ∠С = 180° - ∠D = 180 - 55 = 125°.
∠ACB = ∠C - 90°, так как ∠ACD = 90° (дано).
∠ACB = 125° - 90° = 35°.
Треугольник АВС равнобедренный (АВ=ВС - дано) =>
∠BAC = 35°. Тогда ∠В = 180 - 2·35 = 110° (по сумме внутренних углов треугольника), а ∠А = 180 - 110 = 70° (углы А и В в сумме равны 180°)