меньший катет АС=6см, больший катет ВС=12√3 см
Объяснение:
обозначим вершины треугольника А В С с прямым углом С катетами АС и ВС и гипотенузой АВ. Проекции катетов на гипотенузу образует высота СН проведённая из вершины прямого угла, поэтому СН перпендикулярно АВ. СН также делит ∆АВС на 2 прямоугольных треугольника АСН и СВН в которых АН, ВН, СН - катеты, а АС и ВС - гипотенузы. Он подобны между собой, так как высота проведённая из вершины прямого угла делит его на прямоугольные треугольники подобные между собой и каждый из них подобен ∆АВС. АВ=АН+ВН=6+18=24 см. Рассмотрим ∆АСН и ∆АВС. В ∆АСН АС является гипотенузой, а в ∆АВС - гипотенуза АВ, поэтому гипотенуза АС~ гипотенузе АВ. А также меньший катет ∆АСН АН~ АС(меньшему катету ∆АВС:
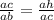
теперь подставим наши значения в эту пропорцию:
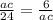
перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:
АС ²=6×24=144
АС=√144=12см
Теперь найдём катет ВС по теореме Пифагора:
ВС²=АВ²–АС²=24²–12²=576–144=432=12√3см

Объяснение:
Вообщем смысл в следующем.
Основная формула объёма цилиндра:
V=πr²*h; πr² - площадь основания цилиндра, h - высота
V=πr²*h , V=π * OB² * OO₁
Треугольник AOB - равнобедренный, так OA=OB как радиусы основания.
OH - это расстояние от центра O до хорды АВ и является высотой-медианой равнобедренного треугольника, и делит сторону АВ пополам под прямым углом.
Дальше, зная высоту ОН=d и НВ (= 1/2 длины хорды АВ) :
(1) по теореме Пифагора (с²=a²+b²) можно найти сторону ОВ как гипотенузу треугольника НОВ:
ОВ²=d²+HB²; ОВ = √(d²+HB²)
(2) Либо через sin угла α (который ∠АОВ), не зря же нам его величину α дали.
sinα - это отношение противолежащего этому углу катета к гипотенузе
[не забываем, что это ∠АОВ = α, а ∠АОВ = α/2 или =1/2α
то есть sin(1/2α) = НВ/ОВ, отсюда чтобы найти радиус ОВ = НВ / (1/2α).
Высота цилиндра и радиус основания образуют другой прямоугольный треугольник O₁ВО, в котором ∠O - прямой (+90°), ∠В = φ
Зная расстояние от верхнего центра до конца хорды O₁В и радиус ОВ (=r), можно найти высоту O₁О, опять же либо по теореме Пифагора, либо через косинус данного угла ∠O₁ОО = φ.
cosφ - отношение прилежащего катета к гипотенузе, то есть
cosφ = O₁О / O₁В, отсюда высота O₁О = O₁В * cosφ
Таким образом, вычислив радиус ОВ основания цилиндра и высоту O₁О цилиндра, сможем найти его объём по формуле: V=πr²*h