Площадь круга, как Вы помните, находят по формуле
S=πr²
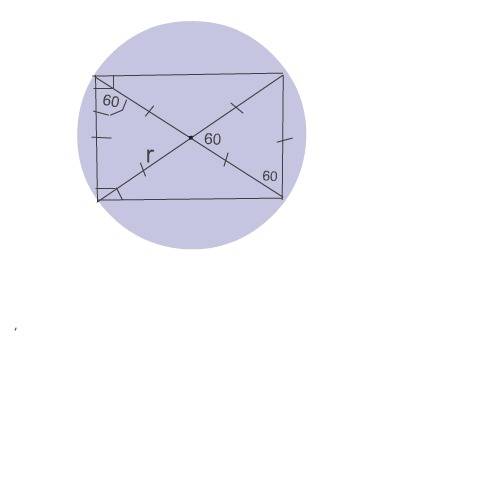
Радиус находим из остроугольных треугольников, образовавшимися диагоналями при меньшей стороне прямоугольника.
Эти треугольники - равносторонние, т.к. угол при пересечении диагоналей равен 60°, а сами диагонали делятся пополам и этим образуют равнобедренные треугольники, углы которых при основании, равном меньшей стороне вписанного прямоугольника, тоже равны 60°.⇒cледовательно, каждая половина диагонали равна меньшей стороне прямоугольника. А так как диагонали здесь являются диаметрами окружности, то радиус описанного круга тоже равен меньшей стороне прямоугольника.
r=10 см
S=πr²,
S=100 π см²
боковая сторона=2,7см
Основание=0,9см
Объяснение:
Основание берём за х
=> боковая сторона 3х
Так как треугольник равнобедренный боковые стороны равны
х+3х+3х=6,3
7х=6,3
х=0,9 - основание
0,9*3=2,7 -боковая сторона
Проверяем:
2,7+2,7+0,9=6,3