Два перпендикулярных отрезка KM и LN пересекаются в общей серединной точке P и образуют два равных треугольника KPN и MPL. Расстояние между точками K и L равно 19,8 см. Какое расстояние между точками M и N?
1. У равных треугольников все соответственные элементы равны, стороны KP =
и NP =
как соответственные стороны равных треугольников.
∡К
=
° и ∡
=
°, так как смежные с ними углы ∡ KPN = ∡ MPL =
°.
По первому признаку треугольник KPL равен треугольнику
.
2. В равных треугольниках соответственные стороны равны. Для стороны KL соответственная сторона — MN.
MN =
см.
1. Сторона, лежащая против угла ∡M:
MA
AR
RM
2. Угол, лежащий против стороны RM:
∡M
∡A
∡R
3. Углы, прилежащие к стороне AR:
∡M;∡A
∡R;∡M
∡A;∡R
Точка пересечения O — серединная точка для обоих отрезков NG и RV.
Как исполняется первый признак равенства треугольников NOR и GOV?
Так как отрезки делятся пополам, то
1. сторона RO в треугольнике NOR равна стороне
в треугольнике
.
2. Сторона NO в треугольнике NOR равна стороне
в треугольнике
.
Угoл NOR равен углу
как вертикальный угол.
Треугольники равны по первому признаку равенства треугольников.
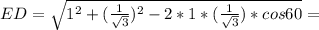
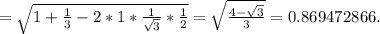
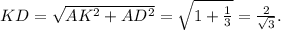
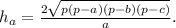
AB=CB =x ; BC=AD =7x ;AB₁ =BA₁ =CD₁=DC₁=13 см ;AD₁ =DA₁ =BC₁=CB₁ =37 см.
обозн._ высота параллелепипеда AA₁ =BB₁ =CC₁ =DD₁ =h.
Sбок - ?
S бок =2(AB+BC)*AA₁ = 2(x+7x)*h =16xh.
По теореме Пифагора для треугольников ABB₁ и ADD₁:
{ AB²+BB₁² =AB₁² ; AD² +DD₁²=AD₁².
{ x²+h² =13² ; (7x)² +h²=37².
Вычитаем из второго уравнения системы первое
(7x)² -x² =37² -13²;
48x² =(37-13)(37+13) ;
2*24x² =24*2*25⇒x =5 ;
h =√(13² -5²) =12.
S бок =16xh =16*5*12 =16*60 =960 (см²).
ответ: 960 см².