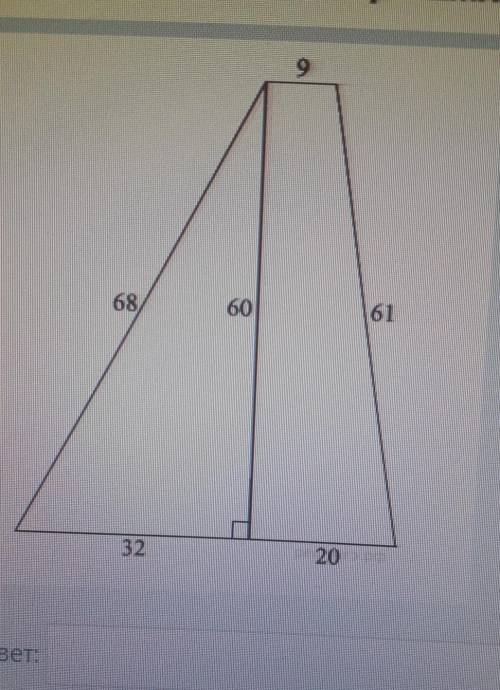
1. 
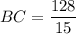
2. 
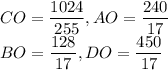
Объяснение:
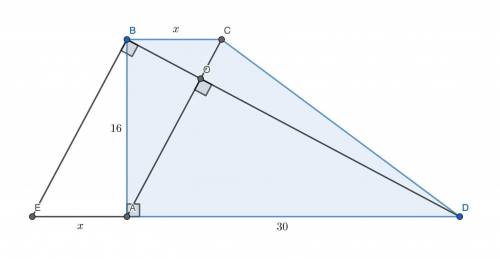
1. Отложим от точки B отрезок BE такой, что он лежит на прямой, параллельной AC, а точка E лежит на прямой AD (то есть выполним параллельный перенос отрезка AC на вектор CB). Поскольку EA || BC как прямые, содержащие основания трапеции, а AC || BE по построению, то AEBC — параллелограмм, откуда BC = EA. Поскольку углы ∠AOD и ∠EBD соответственные при параллельных прямых AC и EB, то они равны, а значит, EB ⊥ BD. Но BA ⊥ ED по условию, значит, в прямоугольном ΔEBD BA — высота, опущенная из прямого угла. Тогда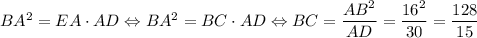 
.
2. В прямоугольном ΔABD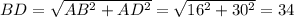 
. В прямоугольном ΔABC 
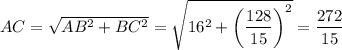. AO — высота, опущенная из прямого угла, 
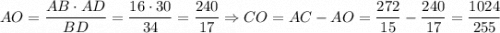. Аналогично 
.
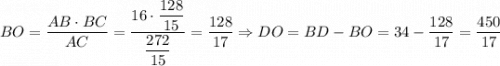" Дан куб abcda1b1c1d1. докажите, что плоскость bdc1 параллельна плоскости ab1d1"
Объяснение:
В плоскости АВ₁D₁ возьмем две пересекающиеся прямые В₁D₁ и АВ₁. Этим прямым в плоскости ВDС₁ будут параллельны прямые ВD и DC₁
( по свойству параллельности противоположных граней куба). Тогда (АВ₁D₁)║( ВDС₁ ) ,по признаку параллельности плоскостей.
Признак параллельности плоскостей : Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
Формула нахождения площади трапеции:
В этом случае:
ответ: 1830