биссектриса угла в параллелограмме отсекает от него равнобедренный треугольник, поэтому треугольник АВК равнобедренный, АВ=ВК. Тогда сторона ВС=7+8=15. АВ=7, периметр АВСД=(АВ+ВС)*2=(15+7)*2=44. Если бы не знали точно, какой отрезок 7, а какой 8,то был бы ещё случай АВ=8, ВС=15 Р(АВСД)=)(8+15)*2=46
1) если в четырехугольник можно вписать окружность, то сумма его противолежащих углов = 180 град. ∠Р и ∠Н являются противолежащими. получим, что ∠Н= 180- ∠Р= 180-120=60град.
2) проведем высоту КА. рассмотрим ΔКАН:
а) треуг прямоуг, тк ∠А= 90 град( высота)
б) по тригонометрическим формулам в прямоуг. треуг. катет= гипотенуза* cos прилежащего угла. АН= 6*cos 60= 6*1\2=3см
в) по тригонометрическим формулам КА= 6*sin противолежащего угла= 6*sin 60=6*√3\2= 3√3см
3) рассмотрим ΔМКА
а) треуг прямоуг (высота)
б) по теореме катет, лежащий против угла в 30 град, равен половине гипотенузы. получим, что МК= 3√3*2=6√3см
4) залезем в ΔМКН .мы можем сказать, что этот треуг вписан в окружность. если мы применим теорему синусов в этом треуг, по найдем радиус. итак, теорема синусов: 2R=а\sinА, где а- сторона треуг, а ∠а- противолежащий угол для этой стороны. 2R=МК\sin 60=6√3: √3\2=6√3*2\√3=12. 2R=12. тогда R= 12\2=6см
ответ:6

Заметим, что треугольник АВС - равнобедренный, так как угол ВКА равен углу КАD, как накрест лежащие углы при параллельных прямых. А в свою очередь угол КАD равен углу ВКА по определению биссектрисы. Значит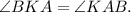 Поэтому треугольник АВК - равнобедренный. Значит стороны АВ и ВК равны. АВ=ВК=7 см.
Поэтому треугольник АВК - равнобедренный. Значит стороны АВ и ВК равны. АВ=ВК=7 см.
Периметр параллелограмма равен
2*АВ+2*ВС=2*7+2*(ВК+КС)=14+2*(7+8)=14+2*15=14+30=44 см