Даны точки: AC – 6; 1), B(-2; 5), C (5; — 2), D(1; — 6) Найти: а) координаты векторов AB, CD б) длину вектора ВС
в) координаты точки M— середины AB и координаты точки N — середины CD
г) уравнение окружности с радиусом BC
д) уравнение прямой BD
е) докажите, что векторы AB и CD коллинеарные
ж) докажите, что ABCD -прямоугольник.
ИНАЧЕ 2 В ГОДУ ВЫЙДЕТ
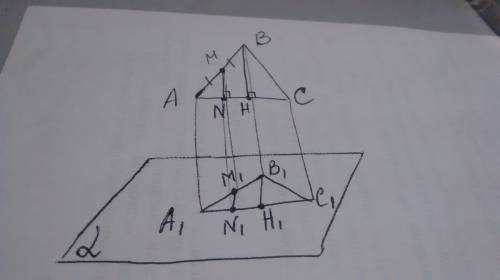
1. Обозначим точки пересечения с прямой L: А1 и В1 соответственно точкам А и В. Расстояние от точки до прямой определяется длиной перпендикуляра, следовательно, надо найти АА1. Когда сделаем чертеж, получим прямоугольную трапецию АА1ВВ1. Обозначим точку на прямой l M1. То есть: АА1, BB1 и MM1 ⊥ L, и AA1, MM1 и ВВ1 ║L.
2. Зная, что АМ=МВ (по условию) и АА1, ММ1 и ВВ1 ║а (п. 1) получим: А1М1=М1В1 (по теореме Фалеса).
3. Найдем АА1 по формуле средней линии трапеции: (АА1+12)/2=16, отсюда АА1 = 20 см.
ответ: 20 см