Объяснение: постаралась выделить цветом))
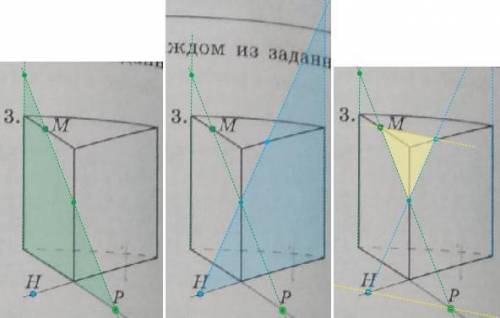
первое, что ищем - точки, лежащие в одной плоскости.
их можно соединить, получим прямую линию, которая, пересекаясь с ребрами призмы (пирамиды), даст возможность перехода из одной грани (плоскости) в другую...
ребро (линия пересечения плоскостей) - множество точек, лежащих в двух плоскостях...
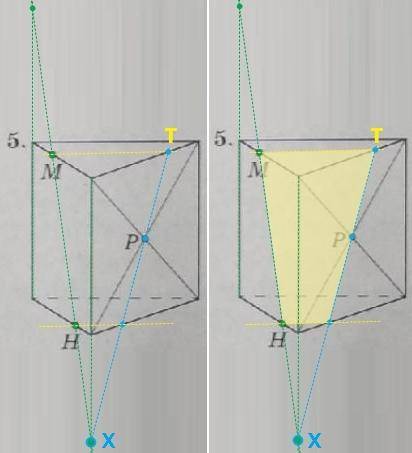
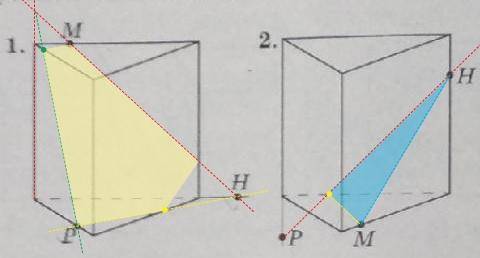
5. видим: точки М и Н лежат в одной плоскости
(зелененькие; левая боковая грань); прямая МН может пересечься с вертикальными ребрами (линиями, лежащими в этой же плоскости !) и одна из двух точек пересечения (X) окажется в той же плоскости,
что и Р (в правой боковой грани; синий цвет) =>
эти две точки (одну новую X и Р) можно соединить (они лежат в одной плоскости) и линия РХ даст новые точки пересечения с ребрами (границами с верхним и нижним основанием)... одну точку обозначила (Т)-она лежит в одной плоскости с М (в верхнем основании... их можно соединить); другую не обозначила, но ее можно соединить с Н - они обе лежат в нижнем основании... сечение-четырехугольник.
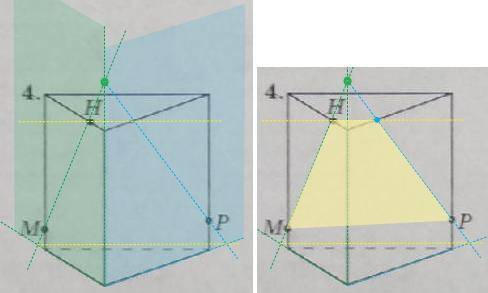
сечение - это часть плоскости (многоугольник), стороны которого лежат в гранях (плоскостях) многогранника (призмы, пирамиды);
или сечение - это часть плоскости, ограниченная линиями пересечения с гранями многогранника (призмы, пирамиды).
проверка: линии пересечения плоскости-сечения с параллельными плоскостями (основаниями) будут параллельны (желтые линии).
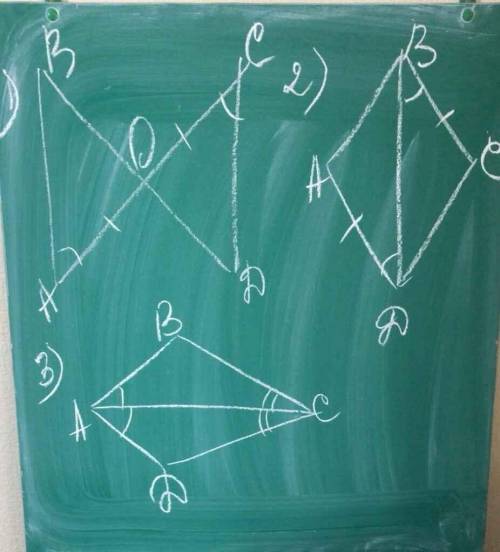
1)
По условию CH - высота, ∠CHB=90°
Рассмотрим прямоугольный треугольник CBH.
Синус угла B - отношение противолежащего катета CH к гипотенузе CB.
sinB =CH/CB => CH =CB sin30° =10√3 *1/2 =5√3
Косинус угла B - отношение прилежащего катета HB к гипотенузе CB.
cosB =HB/CB => HB =CB cos30° =10√3 *√3/2 =15
S(ABC) =1/2 AB*CH =1/2 (5+15) *5√3 =50√3
(площадь измеряется в квадратных единицах)
2)
В прямоугольном треугольнике
сторона против прямого угла - гипотенуза
стороны, прилегающие к прямому углу - катеты.
∠C=90, AB - гипотенуза
AC, BC - катеты
Синус острого угла - отношение противолежащего катета к гипотенузе.
sinA =BC/AB =5√3/10 =√3/2
Косинус острого угла - отношение прилежащего катета к гипотенузе.
cosA =AC/AB =5/10 =1/2
sinB =AC/AB =1/2
cosB =BC/AB =√3/2
A=60°, B=30°
В треугольнике с углами 30, 60, 90 стороны относятся как 1:√3:2