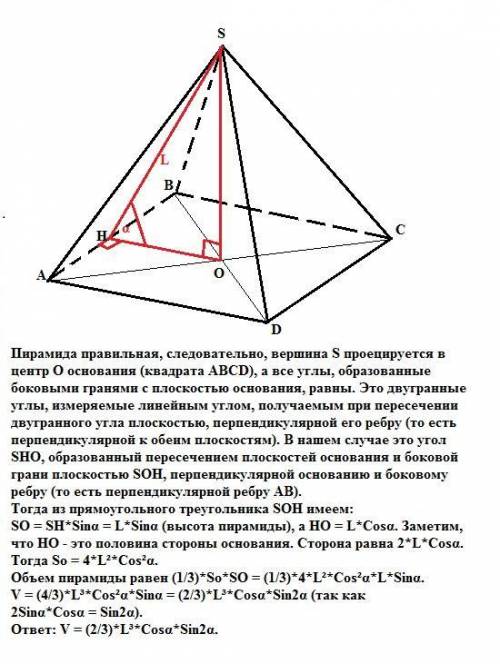
Пирамида правильная, следовательно, вершина S проецируется в центр О основания (квадрата АВСD), а все углы, образованные боковыми гранями с плоскостью основания, равны. Это двугранные углы, измеряемые линейным углом, получаемым при пересечении двугранного угла плоскостью, перпендикулярной его ребру (то есть перпендикулярной к обеим плоскостям). В нашем случае это угол SHO, образованный пересечением плоскостей основания и боковой грани плоскостью SOH, перпендикулярной основанию и боковому ребру (то есть перпендикулярной ребру АВ).
Тогда из прямоугольного треугольника SOH имеем:
SO = SH*Sinα = L*Sinα (высота пирамиды), а НО = L*Соsα.
Заметим, что НО - это половина стороны основания. Сторона равна 2*L*Соsα.
Тогда площадь основания So = 4*L²*Соs²α.
Объем пирамиды равен (1/3)*So*SO = (1/3)*4*L²*Соs²α*L*Sinα.
V = (4/3)*L³*Соs²α*Sinα = (2/3)*L³*Соsα*Sin2α (так как
2Sinα*Cosα = Sin2α).
ответ: V = (2/3)*L³*Соsα*Sin2α.
Ортоцентр H треугольника ABC отразили относительно сторон и получили точки A₁, B₁ и C₁. Найдите углы треугольника A′B′C′, если ∠A=50∘, ∠B=75∘.
Объяснение:
По свойству ортоцентра : "Точка, симметричная ортоцентру относительно стороны треугольника, лежит на описанной около него окружности". Значит все точки А, В, С,A₁, B₁ , C₁-лежат на окружности.
1)ΔАВМ -прямоугольный ,∠А=50°⇒ ∠АВМ=90°-50°=40° . Значит ∠МВС=75°-40°=35° .Поэтому дуги ∪ АВ₁=80° и ∪ В₁С=70° по т. о вписанном угле.
2)ΔАСР -прямоугольный ,∠А=50°⇒ ∠АСР=90°-50°=40° . Значит ∠РСВ=55°-40°=15° .Поэтому дуги ∪ АС₁=80° и ∪ С₁В=30° по т. о вписанном угле.
3)ΔАВК -прямоугольный ,∠В=75°⇒ ∠ВАК=90°-75°=15° . Значит ∠САК=50°-15°=35° .Поэтому дуги ∪ СА₁=70° и ∪ А₁В=30° по т. о вписанном угле.
)ΔА₁В₁С₁ , по т. о вписанном угле : ∠А₁=1/2*(80°+80)°=80° ,∠В₁=1/2*(30°+30)°=30° , ∠С₁=1/2*(70°+70)°=70°.