Теорема Пифагора действительно только для прямоугольных треугольников. Она выглядит так - а^2 + b^2 = c^2
Т. е. первый катет^2 + второй катет^2 = гипотенуза^2
Если нам неизвестен какой-либо из катет пользуемся правилом суммы. (Чтоб найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое). И получится
a^2 = c^2 -b^2; либо
b^2 = c^2 - а^2 .
№1 Возьмём прямоугольный треугольник, у которого первый катет равен 15 см, второй - 8 см, а гипотенуза равна 17 см. Предположим нам неизвестен первый катет. И тут мы берём теорему Пифагора
а^2 + b^2 = c^2
Так как нам неизвестен катет пользуемся правилом суммы и у нас получается :
a^2 = c^2 -b^2
Подставляем числа:
a^2 = 17^2 - 8^2
a^2 = 289 - 64 = 225
Извлекаем корень из 225.
a = 15 см. Что и требовалось доказать.
№2 Возьмём прямоугольный треугольник, у которого первый катет равен 8 см, второй катет - 6 см, гипотенуза - 10 см.
Предположим нам надо найти гипотенузу
а^2 + b^2 = c^2
8^2 + 6^2 = а^2 + b^2 = c^2
64 + 36 = c^2
100 = c^2
Извлекаем корень из 100.
с = 10 что и требовалось доказать.
Есть проще -
8^2 + 6^2 = 10^2
100 = 100
Что и требовалось доказать.
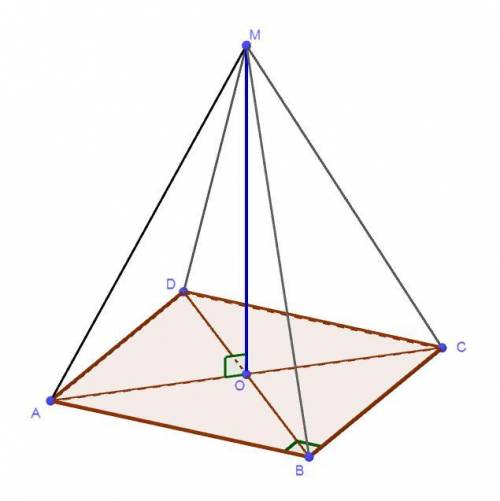
Точка пересечения диагоналей квадрата является центром квадрата. Т.к. из него проведена перпендикулярная прямая, значит расстояние от т. О до вершин квадрата будет одинаковое. Следовательно, нам нужно найти одно такое расстояние, чтобы знать все.
Стороны квадрата (а) равны. Диагонали у квадрата равные (d), и точк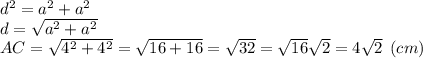 а пересечения делит их пополам.
а пересечения делит их пополам.
Р-м ΔAOM:
∠O = 90°, AO — половина диагонали, OM — перпендикуляр к плоскости квадрата. АМ — наклонная.
AO = d/2
Ищем, чему равна диагональ квадрата:
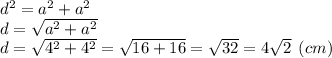
AO = (4√2)/2 = 2√2 см
Теперь можем найти длину отрезка AM
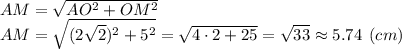
ответ: Расстояние равно √33 см, или приблизительно 5,74 см.
вроде все четко)
строишь это бред, берем верхнее основание цилиндра, там получается треугольник АВО, где О-центр окружности, А и В-вершины сечения,
в треуголнике АВО, ОА=ОВ=R, и угол АОВ=2а, и еще высота ОН= D, высота в равнобедренном и медиана и биссектриса, то бишь АОН= а, значит OA=R=D/cos(a)
откуда АВ= 2* корень из (D/cos(a))^2 -D^2= 2D*(корень из 1- cos^2(a))/cos(a)=2D*sin(a)/cos(a)= 2D*tg(a)
сечение это прямоугольник, пусть АВН1Н, значит треугольник АНВ-прямоугольный, и угол АНВ=у, тогда АН=Н=AB/tg(y)=2D*tg(a)/tg(y)
V=pi*R^2*H
V=pi*D^2/cos^2(a) * 2D*tg(a)/tg(y) ну и как раз твой ответ