Если из внешней точки к окружности проведены касательная и секущая, то квадрат отрезка касательной от данной точки до точки касания равен произведению длин отрезков секущей от данной точки до точек её пересечения с окружностью.
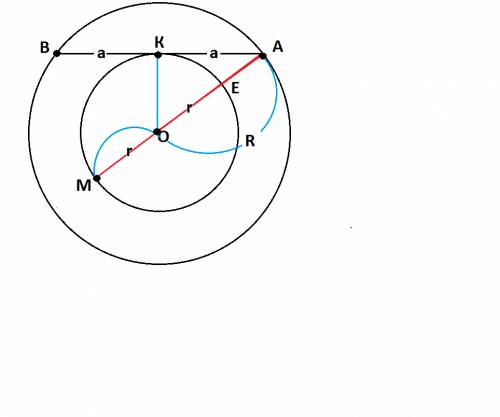
Для меньшей окружности точка А на большей окружности является внешней точкой.
АК²=АЕ*АМ
АЕ=R-r
AM=R+r
Пусть АК=а.
Тогда а²=(R-r)(R+r)=(R² -r²)
Т=π(R² -r²)⇒
Т=π*а²⇒
а=√(Т/π)
АВ=1а=2√(Т/π)
BC - горизонтальный. Пусть AC>BC
CM - медиана
СК - высота. Тр-ник CKM - прямоугольный; K=90
1) Угол KCM=3 гр.⇒угол CMK=90-3=87
Медиана в прямоугольном тр=ке является радиусом описанной окружности⇒
AM=CM=MB⇒тр-ник CMB - равнобедренный⇒углы MCB и MBC равны.
угол MCB + угол MBC=180-угол CMB=180-87=93⇒
угол CMB=углу B=93/2=46 гр 30 мин
угол A=90-46 гр 30мин=43 гр 30 мин
2)Угол KCM=22 гр.⇒угол CMK=90-22=68
Медиана в прямоугольном тр=ке является радиусом описанной окружности⇒
AM=CM=MB⇒тр-ник CMB - равнобедренный⇒углы MCB и MBC равны.
угол MCB + угол MBC=180-угол CMB=180-68=112⇒
угол CMB=углу B=112/2=56
угол A=90-56 =34
B=56 - больший угол