Треугольник СДЕ прямоугольный и равнобедренный, так как СЕ высота трапеции, а угол СДЕ равен 450, тогда СЕ = ЕД = 4 см.
Так как BF высота трапеции, то BF = СЕ = 4 см, а треугольник АВF прямоугольный, тогда: tg60 = BF / AF. AF = BF / tg60 = 4 / √3 см.
Длина отрезка EF = ВС = 5 см, тогда АД = AF + EF + ДЕ = 4 / √3 + 5 + 4 = 9 + 4 / √3 см.
Определим площадь трапеции:
Sавсд = (ВС + АД) * СЕ / 2 = (5 + 9 + 4 / √3) * 4 / 2 = 28 + 8 / √3 = (84 + 8 * √3) / 3 см2.
ответ: Площадь трапеции равна (84 + 8 * √3) / 3 см2
как то так =)
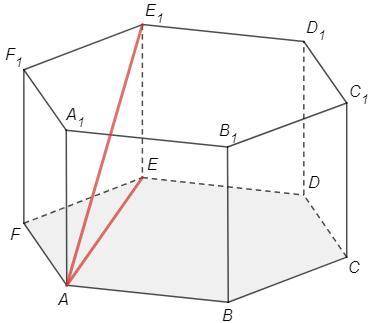
Правильная шестиугольная призма - в основании правильный шестиугольник, боковые ребра перпендикулярны основанию.
Угол между прямой и плоскостью - угол между прямой и ее проекцией.
1) EE1⊥(ABC) => AE - проекция наклонной AE1 на плоскость (ABC)
∠E1AE - угол между AE1 и (ABC)
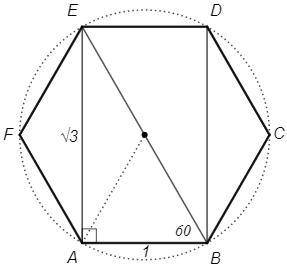
∠ABE=60 (правильный шестиугольник)
AE =AB tg(ABE) =1*tg60 =√3
tg(E1AE) =EE1/AE =1/√3 => ∠E1AE=30°
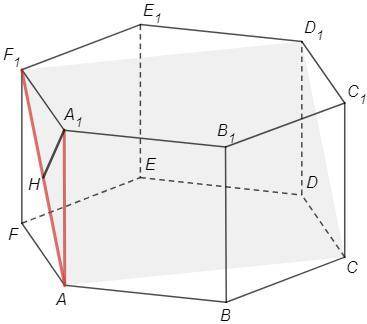
2) ABDE и ABD1E1 - прямоугольники (ABDE - проекция ABD1E1)
=> AB⊥AE1, AB⊥AE => AB⊥(AEE1)
Опустим A1G⊥AE1
AB⊥(AEE1) => AB⊥A1G
A1G⊥AB, A1G⊥AE1 => A1G⊥(AE1D1)
∠A1BG - угол между BA1 и (AE1D1)
∠E1AE=30 => ∠A1AG=60
A1G =AA1 sin(A1AG) =1*sin60 =√3/2
BA1=√2 (диагональ квадрата)
sin(A1BG) =A1G/BA1 =√3/2 :√2 =√6/4
∠A1BG =arcsin√6/4 ~37,76°
3) Аналогично пункту 2
ACDF и ACD1F1 - прямоугольники => AC⊥(FAA1)
Опустим A1H⊥AF1
AC⊥(FAA1) => AC⊥A1H
A1H⊥AF1, A1H⊥AC => A1H⊥(AF1D1)
∠A1AF1 - угол между AA1 и (AF1D1)
∠A1AF1=45° (AF1 - диагональ квадрата)

Сечения изображены на 1 и 3 рисунках.
На 1 рис. сечение A₁С₁D , на 3 рис. сечение AEFD , так как на рисунках показаны линии пересечения секущей плоскости с гранями параллепипеда .