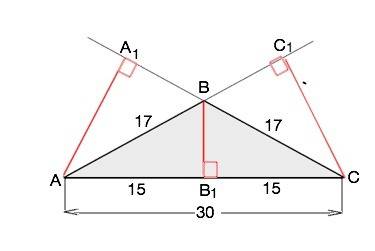
Назовём данный треугольник АВС.
ВВ1- высота к АС.
АА1=СС1 - высоты к равным боковым сторонам.
Высота равнобедренного треугольника, проведенная к основанию, является его биссектрисой и медианой. ⇒
АВ1=СВ1=30:2=15 см
∆ АВВ1=∆ СВВ1 ( по трем сторонам).
Из ∆ АВВ1 по т.Пифагора
ВВ1=√(AB²-AB1²)=√(17²-15²)=8 см
Высоты к боковым сторонам найдем из площади ∆ АВС
Заметим, что ∆ АВС - тупоугольный ( АС² > АВ²+ВС²), поэтому высоты, проведенные к боковым сторонам тупоугольного треугольника, лежат вне его.
S(ABC)=BB1•AC:2=8•15=120 см²
AA1=2S(ABC):BC
AA1=CC1= см
см
d^2=a^2+a^2
Подставим значения в формулу:
d^2=6^2+6^2=36+36=72 cm
Высоту h мы найдем с и ребра b:
h=sqrt{{d/2}^2+b^2}
h=sqrt{{{72}/2}^2+5^2}=sqrt{36+25}=sqrt{61}=7,8 cm
Теперь найдем площадь квадрата, который лежит в основании правильной пирамиды:
S=6^2=36{cm}^2
Подставим найденные значения в формулу расчета объема:
V={1/3}*36*7,8=14,6{cm}^3
Если по условиям даны длина ребра c правильной пирамиды и длина стороны основания a, то можно найти значение по следующей формуле:
S_bok={1/2}a sqrt{5^2-{{6^2}/4}}=3*sqrt 16}=12
Площадь всей пирамиды равна:
S=4*S_bok + S_osn= 4*12 + 36=84