∠А = 55°
Объяснение:
ВМ является медианой, следовательно АМ = МС - согласно условию задачи.
Но так как АМ = ВМ (также согласно условию задачи), то МС = ВМ, в силу чего треугольник ВМС - равнобедренный и ∠МВС = ∠С =35°.
Следовательно, угол ВМС равен:
180 - 35 - 35 = 110°.
Из этого следует, что в треугольнике АВМ угол АМВ, смежный с углом ВМС, равен:
180 - 110 = 70°.
Треугольник АВМ также является равнобедренным, т.к. АМ = ВМ, и если угол при его вершине равен 70°, то углы при основании (∠А и ∠АВМ) равны:
∠А = ∠АВМ = (180 - 70) : 2 = 110 : 2 = 55°
ответ: ∠А = 55°
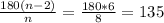градусов, значит, каждый угол восьмиугольника равен 135 градусов. Рассмотрим четырёхугольник АВСН, в нём два угла по 135 градусов и два по х градусов (АВ параллельна СН так как точки А и В равноудалены от точек С и Н, это получилась равнобедренная трапеция). В выпуклом четырёхугольнике сумма углов равна 360 градусов, таким образом 2х=90 градусов, следовательно, х=45 градусов. Отсюда мы можем найти углы DСН и GНС, которые равны по 135-х=90 градусов. Аналогично углы СDG и DGН равны по 90 градусов, значит, CDGH - прямоугольник. Одна сторона этого прямоугольника равна стороне восьмиугольника, теперь найдём вторую.
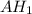и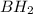 
. 
. 
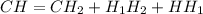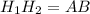, потому что получился прямоугольник, а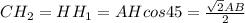 
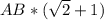
Фото нужно
Объяснение:
Нужно фотографии