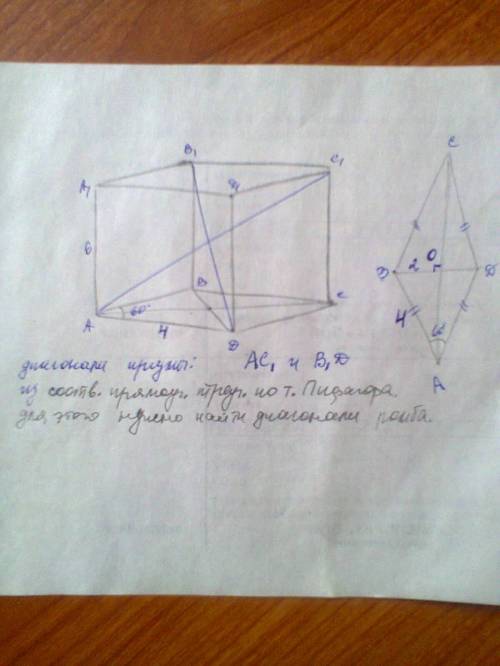
Диагонали ромба точкой пересечения делятся пополам (как и у параллелограмма)
Диагонали ромба взаимно перпендикулярны
Диагонали ромба являются биссектрисами его углов
из треуг.BOA: угол BAO=30, катет BO = 4/2 = 2 (катет против угла в 30 град.=половине гипотенузы) и по т.Пифагора второй катет = корень(4^2-2^2) = 2корень(3)
следовательно, диагонали ромба равны
BD = 2BO = 4
AC = 2AO = 4корень(3)
AC1^2 = AC^2 + CC1^2 = 4*4*3 + 6*6 = 4*(12+9) = 4*21
AC1 = 2корень(21)
B1D^2 = BD^2 + CC1^2 = 4+36 = 40
B1D = 2корень(10)
Объяснение:
2) ∠MNP + ∠N = 180° - как смежные
∠N = 180° - ∠MNP = 180° - 135° = 45°
ΔMNK - равнобедренный, значит ∠M = ∠N = 45°
ответ: 45°
3) ΔАВС прямоугольный, значит АС и ВС - катеты, АВ - гипотенуза
∠А = 30°, а катет, лежащий напротив угла в 30° равен половине гипотенузы ⇒ ВС = 12 / 2 = 6 см
АС² + ВС² = АВ² (по теореме Пифагора) ⇒ АС² = АВ² - ВС²
АС² = 12² - 6² = 144 - 36 = 108
АС = √108 ≈ 10 см
ответ: 10 см
4) ΔАВС прямоугольный, значит АС и ВС - катеты, АВ - гипотенуза
∠В = 30°, а катет, лежащий напротив угла в 30° равен половине гипотенузы ⇒ АВ = 7.5 * 2 = 15 см
ответ: 15 см
5)∠А = ∠МАN - как вертикальные ⇒ ∠А = 27°
Сумма углов треугольника равна 180°
ΔАВС = 180° = ∠А + ∠В + ∠С
∠А = 180° - 90° - 27° = 63°
ответ: 63°
Средняя линиия трапеции равна полусумме оснований, тогда сумма оснований будет равна 5*2=10, периметр - это сумма длин всех сторон трапеции, тогда сумма боковых сторон будет равна 12-10=2. Так как трапеция вписана в окружность ее боковые стороны будут равны, 2:2=1. боковая сторона трапеции равна 1.