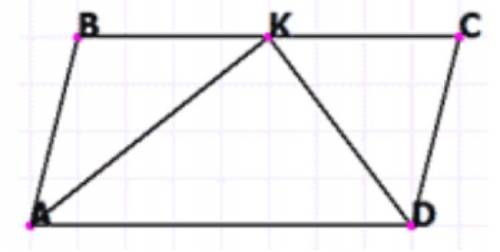
Объяснение:Кут ВАК=кутуКАД, бо АК- бісектриса.Кут КАД=кутуАКВяк вн різностор. тому тр. ВК рівнобедр. АВ=ВК. Аналогічно Кс=СД. АВ+СД=34 см. ВС=АД-34 см. Р=АВ+ВС+СД+АД=34+68=102 см.
1)Пусть АВС-равнобедренный треугольник,АС-основание=12 см.
АВ=ВС=10 см
Проведем высоту ВН
Так как треугольник равнобедренный,то высота,проведенная к основанию,является и медианой,и биссектрисой.
Так как ВН-высота,то образуется прямоугольный треугольник АВН,причем из-за того,что ВН ещё и медиана,то АН=НС=12/2=6см.
Теперь по теореме Пифагора находим катет ВН
ВН=корень из(АВ^2-АН^2)
ВН=корень из(64)
ВН=8см
Sтреугольника АВС=(ВН*АС)/2
S=(8*12)/2
S=48 кв. см
ответ:48 кв.см.
2)параллелограмм ABCD
Проведём из угла В на AD высоту BK.
∆ABK-прямоугольный. ےА=30°
Следовательно BK=AB:2, как катет, лежащий против угла 30°
AB=12. Тогда BK=6; S=16×6=96 кв.см.
ответ:96 кв.см.
3)Дано:
АВСD-трапеция,
АВ=СD=13 см.
АD=20см
ВС=10см
Найти:S
Проводим высоту ВН,так как трапеция равнобедренная,то АН будет равен (20-10)/2=5 см
Образовался прямоугольный треугольник АВН,находим катет(высоту) ВН
ВН=корень из(АВ^2-AH^2)
ВН=корень из(169-25)
ВН=12 см.
S=((АD+ВС)/2)*ВН
S((20+10)/2)*12=180 кв.см.
ответ:180 кв.см
Подробнее - на -
Объяснение:
1) Диагонали параллелограмма равны. НЕВЕРНО
Диагонали равны только у разновидностей параллелограмма : у прямоугольника и квадрата.
2) Катет прямоугольного треугольника, лежащий против угла 30°, равен половине гипотенузы. ВЕРНО
3) В прямоугольной трапеции ровно один прямой угол. НЕВЕРНО
Боковая сторона, которая образует прямой угол с одним основанием трапеции, является перпендикуляром к двум параллельным основаниям, значит, она образует прямой угол со вторым основанием тоже. Всего в прямоугольной трапеции 2 прямых угла. Если в трапеции будет 4 прямых угла, то это будет прямоугольник.
4) Сумма углов четырёхугольника равна 360°. ВЕРНО
ответ будет равен 68.