Если вас еще интересует решение этой задачи, то здесь не так уж и сложно.
Нужно воспользоваться формулами для нахождения диагоналей параллелограмма через его стороны.
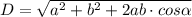
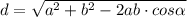
D - большая диагональ, d - малая диагональ.
Подставляем длины сторон и диагоналей и находим угол 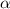
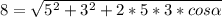
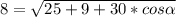
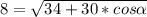
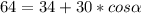
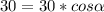
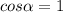

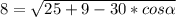

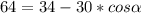
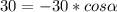
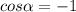
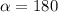
Как видим, углов между сторонами 5 и 3, при которых одна из диагоналей могла бы равняться 8, и при которых сещуствовал бы параллелограмм, нет.
Вот и вывод: диагональ параллелограмма не может равняться 8 при сторонах 5 и 3.
Р=4a
Обозначим высоту ВН, точку ее пересечения с диагональю - М.
Треугольник АВН - прямоугольный.
Пусть АН =х
ВН=10+6=16
Тогда АВ² =ВН² +АН² =256+х²
АВ =√(256+х²)
Рассмотрим ⊿ АМН и ⊿ ВМС - оба прямоугольные, их острые углы равны, ⇒ они подобны
АН:ВС=НМ:ВМ
ВС=АВ⇒
ВС =√(256+х²)
Из подобия треугольников:
х:√(256+х² )=6:10
6х=10√(256+х² )
Возведя обе части в квадрат, получим:
36х² =100(256+х² )
36х² =25600+100х²
64х² =25600
х² =400
х=20
Р=4*20=80 см