
В треугольнике ABC, AB = BC. Медианы треугольника пересекаются в точке O, OA = 5, OB = 6. Найдите площадь треугольника ABC.
============================================================
точка О - точка пересечения медиан ( см приложение )По свойству пересечения медиан в ΔАВС ВО:ОЕ = 2 : 1⇒ ОЕ = ВО/2 = 6/2 = 3 По свойству равнобедренного треугольника ВЕ⊥АС, ВЕ - медиана, высота, биссектрисаВ ΔАОЕ: по теореме ПифагораАЕ² = АО² - ОЕ² = 5² - 3² = 25 - 9 = 16АЕ = 4АС = 2•АE = 2•4 = 8Значит, S abc = BE•AC/2 = 9•8/2 = 36ОТВЕТ: S abc = 36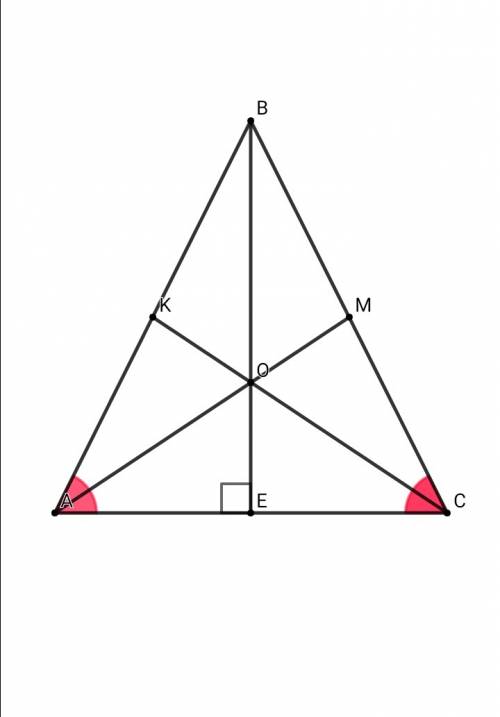
доброй ночи! я понимаю, в чём возникла трудность. но хочу вас заверить — это легко. надеюсь, вы сами это вскоре поймёте.смотрите, чтоб понять, как это делать, нам нужно вспомнить такое понятие как вектор. вектор — направленный отрезок. по условию нам даны координаты вершин треугольника авс. чтоб найти то, что от нас требуется, то первым делом, нам следует найти координаты вектора. в нашем случае — это координаты вектора ab. давайте попробуем найти координаты нужного вектора. но для этого вспомним формулу что и как делать.чтоб найти координаты вектора, надо от точки конца отнять точки начала. вот, когда мы всё это прояснили, то можем приступить к вычислению:
1. 1)VO
2)GVO
2. 1)GO
2)GVO
3)VOG
3. ∠N=63°
∠B=45°