AK = CM
Объяснение:
Имеем углы KAB и MCB. Для начала нужно доказать что эти углы равны, а если эти углы будут равны, то и стороны этих углов тоже будут равны. Первое свойство равнобедренного треугольника гласит: углы при основании равнобедренного треугольника равны. Проведём медиану BD, которая будет делить данный треугольник на равные части. Т.к. углы BAD и BCD равны, то углы KAB и BAD, будут вертикальные, а значит равны. Углы MCB и BCD тоже будут вертикальные, а значит тоже равны между собой. А т.к. углы при основании равны и оба из них имеют равные прилежащие углы, то и углы KAB и MCB, тоже равны!
ответ: 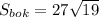
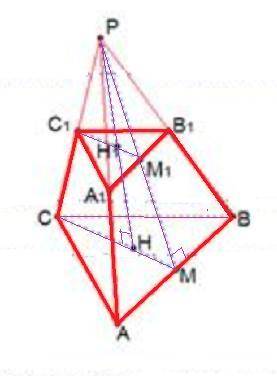
Объяснение: РАВС - правильная треугольная пирамида, АВ=12 , РН=8, А₁В₁С₁║АВС .
АСВ – правильный треугольник, Н – центр данного треугольника (центр вписанной и описанной окружностей). РМ – апофема заданной пирамиды. ММ₁ – апофема усеченной пирамиды. Согласно свойству параллельных плоскостей (две параллельные плоскости пересекают любую третью плоскость так, что линии пересечения параллельны), имеем несколько пар подобных треугольников с равным коэффициентом подобия. В частности
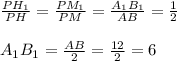
Найдём НМ - радиус вписанной окружности в правильный треугольник:
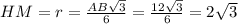
Рассм. ΔРНМ: 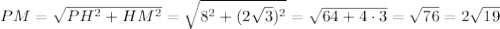
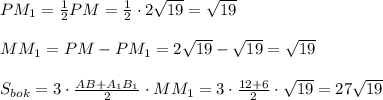
Из прямоугольного треугольника MPH по теореме пифагора:
PH² = PM² - MH²
PH² = 225 - 81
PH² = 144
PH = 12
S = PH*MK
MK = MH + HK = 9+8 = 17
S = 12*17 = 204
ответ: 204