В основании правильной пирамиды - правильный треугольник. Вершина S проецируется в центр О основания. Высота правильного треугольника СН= (√3/2)*а, где а - сторона треугольника. СН=13√3/2. В правильном треугольнике высота=медиана и делится центром в отношении 2:1, считая от вершины. => HO=(1/3)*CH, а СО=(2/3)*СН или СО=13√3/3, НО=13√3/6.
По Пифагору:
Боковое ребро пирамиды SC=√(CO²+SO²) = √(313/3).
Апофема (высота боковой грани) SH=√(НO²+SO²) = √(745/12).
Боковая поверхность Sбок = (1/2)*3*АВ*SH =(39/4)*(√(745/3).
Площадь прямоугольного треугольника равна половине произведения его катетов.
Объяснение:
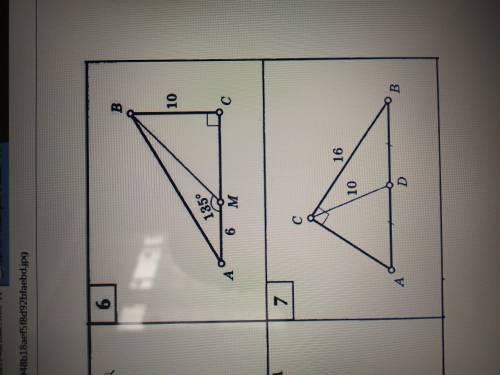
6. Треугольник прямоугольный ВС=10, АС=АМ+МС, АМ=6;
ΔВСМ прямоугольный, ∡М=(180-135)=45° ⇒ ΔВСМ равнобедренный, СМ=ВС=10, АС=6+10=16;
S=16*10/2=80 ед².
7. медиана проведенная к гипотенузе равна её половине.
АВ=10*2=20;
по т. Пифагора АС=√(АС²-АВ²)=√(400-256)=12;
S=12*16/2=96 ед².