Пусть m - прямая, проходящая через точку А, и k - прямая, проходящая через точку В.
Через две параллельные прямые проходит единственная плоскость.
По условию k║m, значит эти прямые лежат в одной плоскости α.
А∈m, m∈α, ⇒ A∈α
B∈k, k∈α, ⇒ B∈α.
Пусть М - точка пересечения прямых m и а, К - точка пересечения прямых k и а.
Тогда точки К и М также лежат в плоскости α.
По аксиоме: если две точки прямой лежат в плоскости, то и все точки прямой лежат в этой плоскости,
значит а∈α.
Итак, точки А, В и прямая а лежат в одной плоскости.

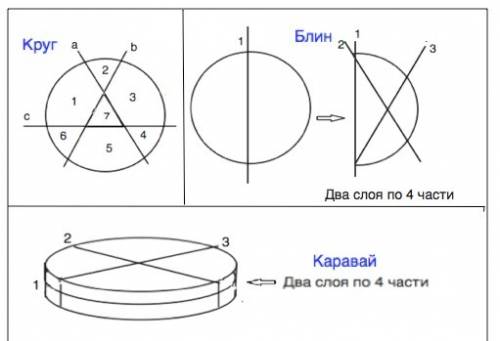
Круг можно тремя разрезами разделить на 7 частей: Линия каждого разреза пересекается с двумя другими и получится 3•2 части, плюс часть, которая получится между ними (см. рисунок).
Блин также можно разделить на 7 частей, если его не сворачивать. Если первым разрезом поделить блин пополам, затем наложить одну половину на другую, а двумя сквозными пересекающимися разрезами разделить эти половини еще на 4 части , то блин можно разделить на 8 частей.
Каравай имеет высоту, на наибольшее количество частей тремя разрезами его можно разделить таким образом:
Первый разрез провести по высоте - получатся две круглые части.
Затем крестообразно провести еще два разреза от края до края и получить наибольшее количество частей, на которое его можно разделить - 8 частей.
Обозначим данный по условию параллелограмм ABCD, AB = 6 см, ВС = 10 см, ∠ В = 150°. ∠А = 180°- ∠В = 180° - 150° = 30° (∠А и ∠В – внутренние односторонние углы при параллельных ВС, AD и секущей АВ). ... Катет ВН расположен напротив ∠А = 30°, значит, равен половине гипотенузы АВ ВН = 3 (см). Находим площадь параллелограмма по формуле: S ABCD = a * h = AD * BH = 10 * 3 = 30 (см²). ответ: площадь параллелограмма 30 см².
Объяснение: