В трапеции АВСD углы, прилежащие к боковой стороне, в сумме равны 180° (как односторонние при параллельных прямых ВС и АD и секущих - боковых сторонах АВ и СD). =>
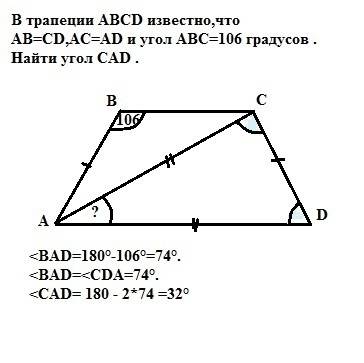
<BAD = 180° - 106° = 74°.
Так как АВ=СD - трапеция равнобедренная, то углы при основаниях равны => <BAD=<CDA = 74°.
Так как AC=AD (дано) => треугольник DAC равнобедренный и углы при основании CD равны. <ACD=<CDA = 74°.
Тогда угол при вершине треугольника САD равен 180-2*74= 32° (так как сумма внутренних углов треугольника равна 180°)
ответ: угол САD=32°.
Используем саму формулу Герона,найдём площадь треугольника
S=корень(р*(р-а)*(р-в)*(р-с))
р(полу-метр)=(8+6+4)/2=9см S²=9*1*3*5=135,тогда S=3*(корень из 15)
2)меньшая высота треугольника Н опущена на большую сторону 8 сантиметров,тогда
S=0,5*8*Н=3*(корень из 15 )Н=0,75(корень из 15)