Решение во вложении.
Т.к AB и CD параллельны и их пересекает прямая BD, то углы ABD и BDC будут равны. В то же время они равны и углу DBC, а значит треугольник DCB является равнобедренным, и CB = DC = 11. Чтобы найти площадь трапеции, можно посчитать площадь прямоугольника ADCH и сложить с площадью квадрата CBH. Либо можно посчитать по стандартной формуле S = (a+b)*h/2. Пойдем вторым путем, для этого надо найти длину BH. Из треугольника CBH по т.Пифагора находим, что она равна корню из 57. Тогда все основание AB равно 11 + корень из 57. Подставляем известные значения в формулу (смотреть вложение) и получаем ответ - 88 + 4 * корень из 57.
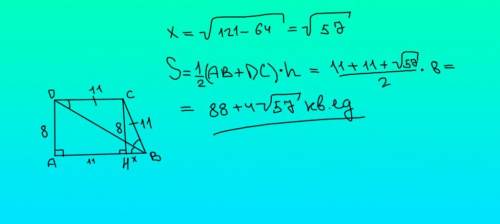
12
Объяснение:
За теоремой про сумму углов треугольника: угол DBA=180°-(90°+30°)=60°.
Угол DBT равен углу ABT (BT - биссектриса), DBT=ABT=60°/2=30°.
В треугольнике DTB: угол TDB (30° за условием) равен углу TBD (30° за решением). Тогда треугольник DTB — равнобедренный (потому что углы при основе DB равные). BT=DT=8.
В треугольнике TAB (угол A=90°):
sin(ABT) = AT/BT
sin(30°) = AT/8
AT = 8*sin(30°) = 8*(1/2) = 4.
(или же, если не умеете через соотношения сторон, можно за свойством катета (AT), который лежит против угла 30° (ABT): AT будет равен половине гипотенузы BT — 8/2=4).
Ну, и DA=DT+AT=8+4=12.