Объём призмы равен значению произведения её высоты и площади основания. Боковое ребро прямой призмы является также и высотой.Площадь трапеции равна значению произведения полусуммы оснований и высоты трапеции.
Трапеция АВСD равнобедренная, значит ее диагонали равны. АС=BD. Проведем прямую СР параллельно диагонали BD до пересечения с продолжением основания AD в точке Р. BCPD параллелограмм и DP=BC. Треугольник АСР прямоугольный и равнобедренный, так как катеты CP и АС перпендикулярны (АС перпендикулярна BD - дано, а CP параллельна BD по построению). Пусть катеты AC и CР равны X. Тогда гипотенуза AP=Х√2 (по Пифагору). CH - высота треугольника АСР, проведенная из вершины прямого угла и равна произведению катетов, деленному на гипотенузу (свойство). Итак, CH=AC*CP/AP. CH=14см (дано). Тогда 14=Х^2/(Х√2). Отсюда Х=14√2, а АР=14√2*√2=28см. Но АР=AD+BC. Тогда площадь трапеции равныS=(AD+BC)*CH/2 или S=28*14/2=196 см^2. ответ: S=196 см^2.
Дано:
ABCDA₁B₁C₁D₁ - прямая призма; ABCD - основание призмы, равнобедренная трапеция; AD - основание трапеции; BC = 5см; AD = 11см; AC = 10см; AC₁ = 26см.
*Все диагонали призмы равны между собой (BD₁=B₁D=AC₁=A₁C), поскольку призма прямая и в основании равнобедренная трапеция.
Найти:
V - ?
В трапеции ABCD:
опустим перпендикуляры BH₁ и CH₂;
BH₁⊥AD, BC║AD ⇒ BCH₂H₁ - прямоугольник;
BC = H₁H₂ = 5см, как противоположные стороны прямоугольника;
трапеция равнобедренная, поэтому AH₁ = H₂D;
AH₁ = (AD-H₁H₂):2 = (11-5):2 = 3 см;
AH₂ = AH₁+H₁H₂ = 3+5 = 8 см.
В прямоугольном ΔAH₂C (∠CH₂A=90°):
AC=10см; AH₂=8см;
По теореме Пифагора:
(CH₂)² = AC²-(AH₂)²;
(CH₂)² = 10²-8² = 100-64 = 6² см²;
CH₂ = 6см.
CC₁⊥(ABC) т.к. призма прямая; AC⊂(ABC);
Тогда CC₁⊥AC.
В прямоугольном ΔACC₁ (∠ACC₁=90°):
AC₁=26см; AC=10см;
По теореме Пифагора:
(CC₁)² = (AC₁)²-AC²;
(CC₁)² = 26²-10² = (26-10)(26+10) = 16·36 = (4·6)² см²;
CC₁ = 24см.
Объём призмы равен значению произведения её высоты и площади основания. Боковое ребро прямой призмы является также и высотой.Площадь трапеции равна значению произведения полусуммы оснований и высоты трапеции.V = CC₁·S(ABCD) =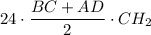 = 12·(5+11)·6 = 72·16 = 1152 см²
= 12·(5+11)·6 = 72·16 = 1152 см²
ответ: 1152см².