S1 ≈ 19,8 cм².
S2 ≈ 3,9 cм².
Объяснение:
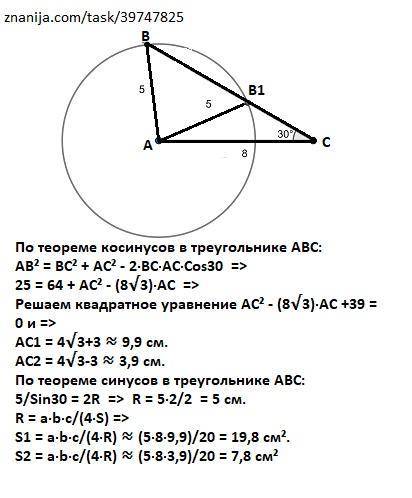
По теореме косинусов в треугольнике АВС:
АВ² = ВС² + АС² - 2·ВС·АС·Сos30 =>
25 = 64 + AC² - (8√3)·AC =>
Решаем квадратное уравнение AC² - (8√3)·AC +39 = 0 и =>
AC1 = 4√3+3 ≈ 9,9 см.
АС2 = 4√3-3 ≈ 3,9 см.
По теореме синусов в треугольнике АВС:
5/Sin30 = 2R => R = 5·2/2 = 5 см.
R = a·b·c/(4·S) =>
S1 = a·b·c/(4·R) ≈ (5·8·9,9)/20 = 19,8 cм².
S2 = a·b·c/(4·R) ≈ (5·8·3,9)/20 = 7,8 cм²
P.S. Для проверки на рисунке выполнено точное построение, доказывающее, что задача имеет два решения.
Задачи на второй признак равенства треугольников
Треугольники
Посмотрев данный видеоурок, все желающие смогут получить представление о теме «Задачи на второй признак равенства треугольников». В ходе этой лекции учащимся предстоит вспомнить, повторить и научиться применять все о втором признаке равенства треугольников. Учитель подробно разберет и решит несколько задач по этой теме.
Сначала вспомним, что две фигуры называются равными, если их можно совместить наложением. Однако очень трудно сравнивать фигуры по определению, поэтому мы введем признаки равенства треугольников – по некоторым элементам.
Объяснение:
найдём длины сторон
АВ=корень из (8-6)^2+(2-7)^2+(6-8)^2= корень из 4+25+4= корень из 33
BC= корень из (4-8)^2+(3-2)^2+(2-6)^2= корень из 16+1+16= корень из 33
CD= корень из (2-4)^2+(8-3)^2+(4-2)^2= корень из 4+25+4= корень из 33
AD= корень из (2-6)^2+(8-7)^2+(4-8)^2= корень из 16+1+16= корень из 33
все стороны равны. Чтобы определить ромб это или квадрат найдём косинус любого угла
cosA=вектор AB * вектор AD / модуль вектора AB* модуль вектора АD
найдём координаты векторов АВ и AD
координаты вектора АВ{2;-5;-2} AD{-4;1;-4}
cosA=2*(-4)+1*(-5)+(-2)*(-4)/ корень из 33 * корень из 33 =-5/33
косинусАчисло отрицательное, значит угол А тупой, поэтому АВСD-ромб