доп построение: ВК(высота)=СН
тогда КВСН-прямоугольник, следовательно ВС=КН=16
Рассмотрим треугольник НСD-он прямоугольный и равен треугольнику АВК(по катету и гипотенузе:ВК=СН, угол ВКА=углу СНD)
по теореме Пифагора найдем НD:
НD^2=CD^2-CH^2
HD=5
т.к треугольник НСD=треугольнику АВК, то АК=HD=5
AD=AK+KH+HD=26 см
Рассмотрим треугольниу ABC-равносторонний(т.к.DABCD-прав. пирамида) OH=CH/3=6/3=2 (см)(в точке пересечения медианы делятся в отношении 2:1 от вершины)
Рассм. треуг. ODH-прямоуг. По теореме Пифагора DH=корень из DO^2+OH^2=корень из 5+4=корень из 9=3 (см)
Sпп=Sбп+Sосн
Рассм. треуг BCH-прямоуг.
sinB=MC/BC
sin60=6/BC
BC=6/(корень из 3/2)(под корнем только 3)=12/корень из 3=12 корней из 3/3=4 корня из 3(см)
Pосн=3*4 корня из 3=12 корней из 3 (см)
Sбп=1/2*DH*Pосн
Sбп=1/2*3*12 корней из 3=18корней из 3(см^2)
Sосн=1/2*CH*AB=1/2*6*4 корня из 3=12корней из3 (см^2)
Sпп=18корней из 3+12 корней из 3= 30 корней из3 (см^2)
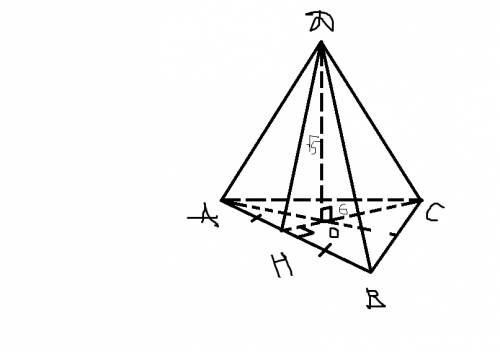
Треугольник CDH прямоугольный, по теореме Пифагора находим сторону √DH=√169-144=5, проведем высоту BK - аналогично, треугольник ABK прямоугольный, AK=5. KH=BC=16. В итоге AD=AK+HD+KH=5+5+16=26/