ответ: 20 см
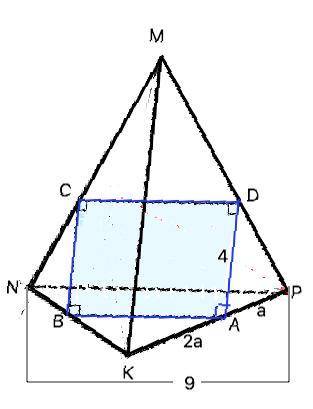
Объяснение: Рассмотрим основание NPK данного тетраэдра. Сторона АВ получившегося прямоугольника параллельна стороне PN треугольника NPK. Треугольники КВА и КNP подобны по двум углам: угол К общий, углы КАВ и КРN равны как соответственные при пересечении параллельных АВ и PN секущей КР.
Из данного в условии отношения отрезков ребра РК примем РА=а, АК=2а, ⇒ РК=РА+АК=а+2а=3а. Коэффициент подобия РК:АК=3:2 . ⇒ PN:АВ=3:2, откуда АВ=2/3 PN=9•2/3=6 дм.
Противоположные стороны прямоугольника равны. Р(АВСD)=2•(АВ+АD)=2•(6+4)=20 (см)
Объяснение:
Из вершины В параллелограмма проведем высоту ВН, которая одновременно высота треугольника АВМ и параллелограмма АВСД.
Воспользуемся формулой площади параллелограмма и выразим из нее высоту ВН.
Sавсд = АД * ВН.
ВН = Sавсд / АД = 60 / АД. (1).
Площадь треугольника АВМ будет равна: Sавм = АМ * ВН / 2.
По условию, АМ / МД = 3 / 2.
3 * МД = 2 * АМ.
МД = 2 * АМ / 3.
АМ = АД – МД.
АМ = АД - 2 * АМ / 3.
АД = 5 * 3 / АМ.
Тогда АМ = 3 * АД / 5.(2).
Подставим выражения 1 и 2 в формулу площади треугольника.
Sавм = (3 * АД / 5) * (60 / АД) / 2 = 180 / 10 = 18 см2.
ответ: Площадь треугольника равна 18 см2.