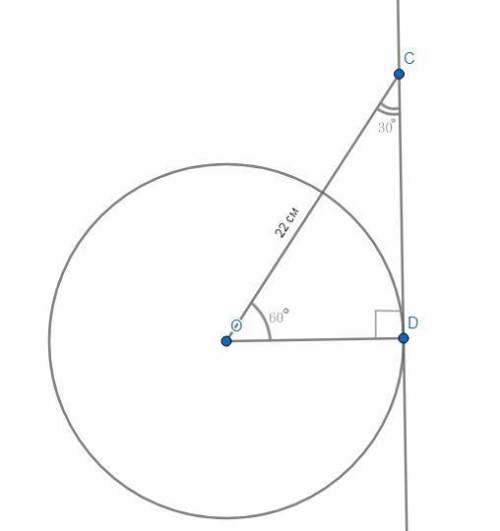
Чертёж смотрите во вложении.
Дано:
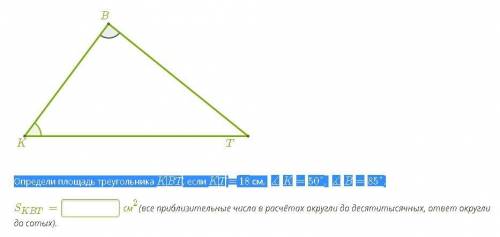
Окружность с центром О.
CD - касательная.
D - точка касания.
OD - радиус.
ОС = 22 см.
∠COD = 60°.
Найти:
ОD = ?
Радиус, проведённый в точку касания перпендикулярен этой касательной. Следовательно, ΔCOD - прямоугольный.Рассмотрим ΔСOD - прямоугольный. ∠OCD = 90°-∠COD = 90°-60° = 30° (так как сумма острых углов прямоугольного треугольника равна 90°). Против угла в 30° лежит катет, равный половине гипотенузы. В нашем случае гипотенуза - СО, так как лежит против угла в 90°. OD - тот самый катет, лежащий против угла в 30°. Поэтому, OD = 0,5*СО = 0,5*22 см = 11 см.ответ: 11 см.
40. 1) Нет, не могут. Углы в 110° и 92° - тупые, а в треугольнике не может быть двух тупых углов (следствие из теоремы о сумме углов треугольника).
2) Да, могут. Угол в 78° - острый, а в 101° - тупой. В треугольнике может быть тупой и острый угол.
(Даже можем сделать проверку. Если мы сложим эти углы (101°+78°), то в сумме получим 179°. Получается, что третий угол равен 1°. Это вполне может быть.)
3) Нет, не могут. Опять же, давайте-ка сразу сложим эти углы. 93°+88° = 181°. Такого категорически не может быть! Сумма двух углов не может превосходить 180°. То есть, получается, что третий угол равен -1°? Такого, опять же, не может быть. Градусная мера угла - строго положительная величина.
4) Нет, не могут. Опять же, сложим эти углы. 170°+12° = 182°. Этого не может быть, так как сумма трёх углов треугольника равна 180°.
ответ: 2).