конус
l (ВМ) = 6 см (образующая)
∠ВМО = 30°
Найти:S осн - ?
Решение:Осевое сечение конуса (секущая проходит через ось конуса) - равнобедренный треугольник, а высота Н (МО) разделяет этот треугольник на два прямоугольных треугольника.
sin(1/2 * 30˚) = R/l
sin(15˚) = R/6
sin(45˚ - 30˚) = R/6
sin(45˚) cos(30˚) - cos(45˚) sin(30˚) = R/6
(√2/3) * (√3/2) - (√2/2) * 1/2 = R/6
(√6/4) - (√2/4) = R/6
((√6) - (√2)) * 6 = 4R
(6√6) - (6√2) = 4R
4R= 6√6 - 6√2
R = (3√6) - (3√2)/2
Итак, ВО (R) = (3√6) - (3√2)/2
S осн = пR²
S осн = п((3√6) - (3√2)/2)² = 18 - 9√3п см²
ответ: 18 - 9√3п см²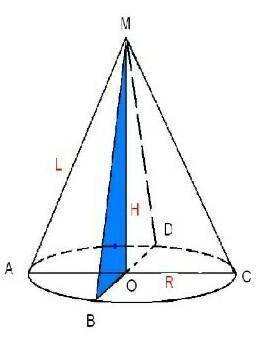
конус
l (ВМ) = 6 см (образующая)
∠ВМО = 30°
Найти:S осн - ?
Решение:Осевое сечение конуса (секущая проходит через ось конуса) - равнобедренный треугольник, а высота Н (МО) разделяет этот треугольник на два прямоугольных треугольника.
sin(1/2 * 30˚) = R/l
sin(15˚) = R/6
sin(45˚ - 30˚) = R/6
sin(45˚) cos(30˚) - cos(45˚) sin(30˚) = R/6
(√2/3) * (√3/2) - (√2/2) * 1/2 = R/6
(√6/4) - (√2/4) = R/6
((√6) - (√2)) * 6 = 4R
(6√6) - (6√2) = 4R
4R= 6√6 - 6√2
R = (3√6) - (3√2)/2
Итак, ВО (R) = (3√6) - (3√2)/2
S осн = пR²
S осн = п((3√6) - (3√2)/2)² = 18 - 9√3п см²
ответ: 18 - 9√3п см²
Предположим, что прямые АС и BD не скрещиваются, тогда они могут быть параллельны или могут пересекаться. Но если прямые параллельны или пересекаются, то в том и другом случае они лежат в одной плоскости. Тогда все четыре точки А, В, С и D лежат в одной плоскости, получается прямые АВ и СD лежат в одной плоскости, но этого не может быть, так как по условию они скрещиваются, а скрещивающиеся прямые не лежат в одной плоскости. Пришли к противоречию, следовательно, предположение о том, что АС и BD параллельны или пересекаются неверно, и данные прямые скрещиваются.