
ответ: ∠1 = 16°; ∠2 = 119°;
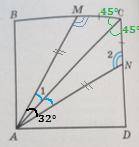
Так как ABCD - это квадрат, то его диагональ AC - это биссектриса. И поэтому прямой угол MCN был разделен на два равных угла биссектрисой AC. Тогда:
∠MCA = ∠NCA = 90° : 2 = 45°.
Теперь докажем, что треугольники MAC и NAC являются равными. У них есть две равные стороны (MC = CN и общая AC) и равные углы (∠MCA = ∠NCA). Поэтому они действительно равны.
И тогда:
∠MAC [угол 1] = ∠NAC = ∠MAN : 2 = 32° : 2 = 16°.
Теперь найдем угол ANC (или угол 2). Воспользуемся тем, что сумма углов треугольника равна 180°:
∠ANC [угол 2] = 180° - ∠CAN - ∠NCA = 180° - 16° - 45° = 119°.
1)АО=СО(по условию)
2)DO=OB(по условию)
3)угол СОВ=углуAOD(как вертикальные)
Из этого следует, что треугольник AOD равен треугольнику СОВ по 1 свойству равенства треугольников.
#2 Докажем что треугольник DMP и DKP равны:
1)DM=DK(по условию)
2)угол MDP=KDP(так как DP - биссектриса)
3)сторона DP - общая
Из этого следует, что треугольник DMP и DKP равны по 1 свойству равенства треугольников.