Дано: Треугольник АВС. АВ=ВСб М∈BD, K∈AC. MK║AB. <ABC=126°,<BAC=27°.
Найти <MKD, <KMD и <MDK.
Решение.
Треугольник АВС равнобедренный, следовательно BD - биссектриса, высота и медиана треугольника. <BAC=<BCA=27°, Значит
<ABD = (1/2)*(<ABC) = 126/2 = 63°. <BDA=<MDK = 90°.
MK параллельна АВ, значит <MKD=<BAC=27°, а <KMD=<ABD=63°, как соответственные углы при параллельных прямых АВ и МК и секущих AD и BD соответственно.
ответ: <MKD=27°, <KMD=63°, <MDK=90°.

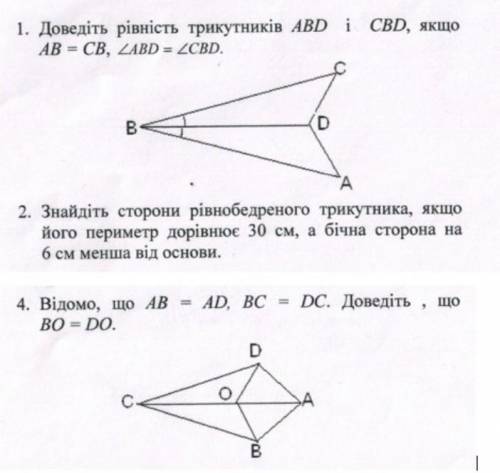
1)Сторона BD - спільна
AB = CB (за умовою)
ABD = CBD (за умовою)
Отже ∆ ABD = ∆ CBD - за 1 ознакою рівності ∆
2) P = 30см
30 : 3 = 10
10 + 6 = 16см (основа)
у рівнобедреному ∆ бічні сторони рівні, тому (30-16):2= 7см
Відповідь: бічні сторони - 7см, основа - 16 см
Объяснение:
хз чи правильно)