Доказательство:
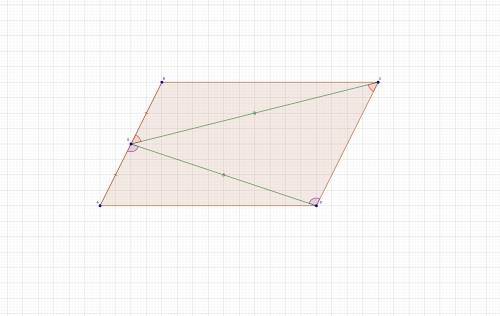
Т.к. ABCD - параллелограмм, то AB//CD и AD//BC.
∠ECD = ∠CEB как накрест лежащие при параллельных прямых AB и CD и секущей EC.
∠EDC = ∠DEA как накрест лежащие при параллельных прямых AB и CD и секущей ED.
Т.к. EC = ED , то ΔECD - равнобедренный с основанием CD.
Значит ∠ECD = ∠EDC как углы при основании.
Следовательно ∠CEB = ∠DEA
ΔEBC = ΔEAD по двум сторонам и углу между ними (EB = EA по условию.)
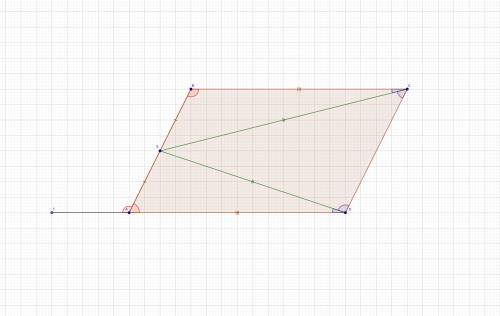
См. рисунок 2.
Из равенства треугольников EBC и EAD следует, что ∠EBC = ∠EAD
и ∠BCE = ∠ADE
∠BCD = ∠BCE + ∠ECD
∠ADC = ∠ADE + ∠EDC
Следовательно ∠BCD = ∠ADC
Продолжим сторону AD влево.
∠FAB = ∠ABC как накрест лежащие при параллельных прямых AD и BC и секущей AB.
∠FAB = ∠ADC как соответственные при параллельных прямых AB и DC и секущей AD
Собирая все вместе получаем, что ∠ABC = ∠BCD = ∠CDA = ∠DAB
Получается, что ABCD - параллелограмм в котором все углы равны. Следовательно ABCD - прямоугольник
@) Сумма углов n-угольника равна 180°(n-2) где n - число сторон!
180°(n-2)=90n решаем уравнение
n=4 (то есть четырехугольник)
180°(n-2)=60n
n=3 треуголльник
180°(n-2)=120n
n=6 ( шестиугольник)
b) Т.к. ∠А=∠C=60°, значит оба угла в сумме составляют 60°+60°=120°.
Известно, что сумма всех углов в любом четырёхугольнике равняется 360°.
Из этого выходит, что сумма ∠B и ∠D = 360°-120°=240°.
Пусть ∠D - x, ∠B - 1,4x.
Зная, что всего 240°, составим уравнение.
x+1,4x=240;
2,4x=240 | : 2,4;
x=100 = ∠D.
∠B=1,4*x=1,4*100=140°.
ответ: ∠D=100°, ∠B=140°.
c) S10=(10-2)×180°=8×180°= 1440° 10 угольника
d)
900
формула такая 180*(n-2), где n - количество углов выпуклого nрямоугольника семиуголника
Объяснение: