1.
A) Прямые не паралельны, так как соответсвующие углы не равны друг другу — а это — 2-ой признак паралельности прямых.
B) Учтить ответ а(одно и то же)
C) Прямые не параллельны, так как по 3-ему признаку параллельности прямых — сумма похожих углов должна быть равна 180^o, а в этом примере их сумма равна 170 градусам.
D) Сумма похожих углов равна 190, а по 3-ему признаку параллельных прямых — должна быть равна 180 градусам, тоесть в нашем случае, прямые не параллельны.
E) Зная два разных соответсвующих угла, мы можем доказать, равны ли два соответствующих друг другу угла: 180-66 = 144^o, что и означает что одна пара соответсвующих углов равна друг другу, тоесть прямые — параллельны(по 2-ому признаку соответсвующих прямых).
2. Зная один похожий угол, мы можем найти другой: 180-«7 => 180-49 = 131^o.
<7 также соответсвующий угол с парой <3, что и означает, что <3 равен <7, тоесть равен 49 градусам. А также поперечные углы равны друг другу(в случае параллельных прямых), значит «2 == <8 => <8 = 131^o.
<1 соответсвует <5-и, тоесть <5 равен 49 градусам.
И так как <2 соответствует <6-и, то <6 = 49^o.
<1 == <7 == <5 == <3 = 49^o
<2 == <6 == <8 == <4 = 131^o.
68. По данным на рисунке найдите площадь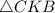
.
- - -Дано :ΔСКВ - прямоугольный (∠С = 90°).
СК - высота (СК⊥АВ).
АК = 4, КВ = 16.
Найти :Следовательно,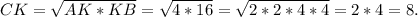
Площадь прямоугольного треугольника равна половине произведения его катетов.Следовательно,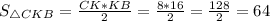
ед².
ответ :64 ед².
- - -70. ABCD - прямоугольник. Найдите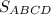
.
- - -Дано :Четырёхугольник ABCD - прямоугольник.
АС - диагональ.
HD⊥АС.
HD = 6, АН = 9.
Найти :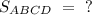
Решение :Прямоугольник - это параллелограмм, все углы которого прямые.Следовательно ∠D = 90°.
Рассмотрим ΔACD - прямоугольный.
В прямоугольном треугольнике высота, опущенная на гипотенузу - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.Следовательно,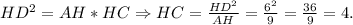
Площадь треугольника равна половине произведения высоты и стороны, на которую опущена эта высота.Следовательно,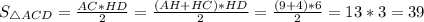
ед².
Диагональ параллелограмма делит параллелограмм на два равновеликих (равных по площади) треугольника.Тогда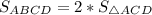
= 2*39 ед² = 78 ед².
ответ :78 ед².