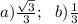
Объяснение:
Смотри прикреплённый рисунок.
Пусть а = 8 см - ребро тетраэдра
a) В основании АВС проведём высоту АЕ ⊥ ВС. АЕ = 0,5а√3;
Опустим высоту SO на плоскость АВС.
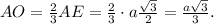
Угол между прямой SA и плоскостью АВС есть угол SAO
b) В основании АВС проведём высоту BK ⊥ AС. BK = 0,5а√3;
Опустим высоту SO на плоскость АВС.
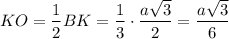
Проведём в грани SAC апофему SK = 0,5а√3
Угол между плоскостями SAC и АВС есть угол SKO между апофемой SK и высотой основания ВК как угол между двумя перпендикулярами, восставленными из точки К к линии пересечения АС плоскостей SAC и АВС
Поскольку тетраэдр правильный, то углы между любой боковой плоскостью и плоскостью основания равны между собой. И косинус между плоскостью SBC и плоскостью АВС равен 1/3.
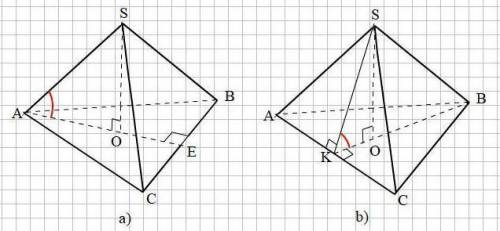
-2х=-12
х=6 - точка пересечения двух линейных ф-ций
у=2х=2*6=12
Координата пересечения (6;12).
Построим первый график у=2х
х=0 у=0 => (0;0)
х=6 у=12 => (6;12)
Построим второй график у=4х-12
х=3 у=0 => (3;0)
х=6 у=12 => (6;12)
Третий график проходит по оси ох, ограничивая два линейных выше, которые пересеклись.
Фигура получилась - треугольник.
Найдем ее площадь как разницу площадей двух прямоугольных треугольников:
SΔAOB=SΔAOC-SΔABC=1/2*12*6-1/2*12*3=1/2(72-36)=1/2*36=18 см²
Можно найти иначе площадь фигуры, через интегралы:
Получили такой же ответ: S=18 см²