Прямоугольник mnke диагональ mk-6cм угол mke=41 градусов найти s прямоугольника )) подробное решение если можно то с рисунком !

👇

Увидеть ответ

Ответ:

maxim090

17.05.2021

Угол МКЕ=углуКМN

угол КМЕ=углу NКМ

так как треугольники МNK=МКЕ равны.

тепрь возьмем угол МКЕ и приймем его за альфу

синус это отношение протиолежащего катета к гипотенузе

следовательно синус альфы = МК / MЕ

sin a=6/ME

sin 41градуса=6/ME

по таблице брадиса синус 41 градуса=0,6561

МЕ=6 / 0,6561

МЕ=примерно 9,1см

теперь возьмем угол КМЕ=49градусам за бету

синус беты=МК / КЕ

sin b=0,7547 по таблице брадиса.

КЕ=6 / 0,7547

КЕ=примерно 8 см

Sпрямоугольника = произведению смежных сторон , т.е. S=a*b = KE*ME

S=8*9,1=72,8 см ^2

ответ: S=72,8 см ^2 (площадь прямоугольника равна 72 целых восемь десятых сантиметров в квадрате)

Прямоугольник mnke диагональ mk-6cм угол mke=41 градусов найти s прямоугольника )) подробное решение

4,6(11 оценок)

Открыть все ответы

Ответ:

khekkp02n6r

17.05.2021

Объяснение:

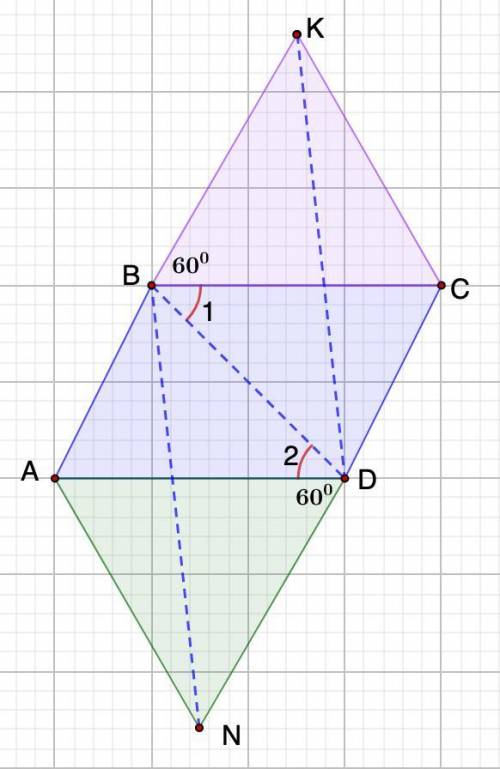
Дано: ABCD - параллелограмм.

ΔВКС и ΔAND - равносторонние.

Доказать: BKDN - параллелограмм.

Доказательство:

1. Рассмотрим ΔВКС и ΔAND - равносторонние.

Противоположные стороны параллелограмма равны.

⇒ ВС = AD

⇒ ΔВКС = ΔAND (по трем сторонам, 3 признак)

⇒ BK = ND

2. ВС || AD (ABCD - параллелограмм)

∠1 = ∠2 (накрест лежащие при ВС || AD и секущей BD)

В равностороннем треугольнике углы равны 60°.

⇒

∠DBK = ∠1 + 60°

∠BDN = ∠2 + 60°

⇒ ∠DBK + ∠BDN - накрест лежащие при BK и ND и секущей BD.

Если при пересечении двух прямых третьей накрест лежащие углы равны, то прямые параллельны.

⇒ BK || ND

Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник - параллелограмм.

⇒ BKDN — параллелограмм

На сторонах параллелограмма ABCD построены равносторонние треугольники BKC и AND. Докажите, что BKDN

4,4(99 оценок)

Ответ:

natakleymyk

17.05.2021

Каноническое уравнение прямой, проходящей через точки
А(х1;у1) и В(х2;у2):
(X-x1)/(x2-x1)=(Y-y1)/(y2-y1).
направляющий вектор этой прямой:
p{p1;p2}, или p{(x2-x1);(y2-y1)}.
Тогда вектор нормали (перпендикуляр к) этой прямой:
n{p2;-p1} или n{(y2-y1);-(x2-x1)}.
Этот же вектор - направляющий вектор для прямой L, проходящей
через точку М((x1+x2)/2;(y1+y2)/2) - середину прямой АВ.
Формула для уравнения прямой, проходящей через точку
M((x1+x2)/2;(y1+y2)/2) и имеющей направляющий вектор
рm{(y2-y1);-(x2-x1)}, то есть уравнение прямой L:
(X-(x1+x2)/2))/(y2-y1)=(Y-(y1+y2)/2)/-(x2-x1) - каноническое уравнение.
Или:
X(x2-x1) + Y(y2-y1) -(1/2)*[x2²-x1²+y2²-y1²] - общее уравнение с коэффициентами А=(x2-x1), В=(y2-y1) и С= -(1/2)*[x2²-x1²+y2²-y1²].

Второй вариант (для тех, кто еще не знает о направляющих и нормальных векторах, но знают о различных видах уравнений прямых):
из канонического уравнения имеем:
X(y2-y1)-x1(y2-y1)=Y(x2-x1)-y1(x2-x1) =>
Y(x2-x1)=X(y2-y1)-y1(x2-x1) =>
Y=X((y2-y1)/(x2-x1) -x1(y2-y1)/(x2-x1)+y1.
Это уравнение прямой с угловым коэффициентом k=(y2-y1)/(x2-x1).
Условие перпендикулярности прямых: k1=-1/k.
Уравнение прямой L, перпендикулярной прямой AB и проходящей через точку М((x2+x1)/2;(y2+y1)/2)) (середина отрезка АВ), находим по формуле:
Y-Ym=k1(X-Xm) или
Y-(y2-y1)/2=-((x2-x1)/(y2-y1))*(X-(x2+x1)/2) отсюда общее уравнение прямой L:
X(x2-x1)+Y(y2-y1)-(y2²-y1²)/2-(x2²-x1²)/2=0 или
X(x2-x1) + Y(y2-y1) -(1/2)*(x2²-x1²+y2²-y1²).

Для проверки решения возьмем точки с реальными координатами и построим график(смотри приложение).

40 выведите уравнение прямой l в прямоугольной системе координат, если l является серединным перпенд