
Одна из формул площади параллелограмма Ѕ=a•h. Очевидно, что при одинаковой площади большей будет высота, проведенная к меньшей стороне, и наоборот. Следовательно, искомой будет высота к стороне АВ ( или равной ей CD).
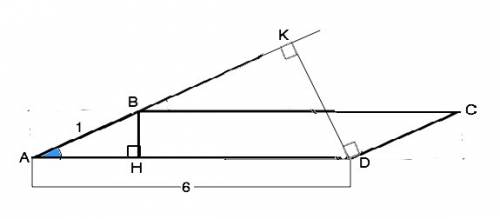
На рисунке в приложении высота к меньшей стороне АВ пересекается с ее продолжением. Из прямоугольного треугольника AKD высота DK=AD•sinA=6•1/3=2 (ед. длины)
Как вариант можно найти большую высоту иначе. Сначала найти длину меньшей высоты ВН=АВ•sinA, затем найти площадь S=ВН•AD и высоту DK=S:AB.
ответ: Р=162 см
Объяснение:
Пусть дана прямоугольная трапеция ABCD. у которой ВС и AD - основания, угол А =углу В=90 градусов. О- центр вписанной в трапецию окружности, точка М - точка касания окружности стороны AD и точка К - точка касания окружности стороны ВС. АМ=20 см, MD=25 см, тогда ОМ=ОК=r=20см и АВ=40 см. DM=DK=25 см как отрезки касательных,проведенных из одной точки. Угол С+ угол D трапеции=180 градусов, как внутренние накрест лежащие углы, DO и CO - биссектрисы соответствующих углов, то угол CDO+DCO=90градусов, следовательно угол COD=90 градусов, т.е. треугольник COD - прямоугольный, у которого ОК - высота, проведенная к гипотенузе, OK^2=DK*CK, CK=400/25=16 см. Значит периметр трапеции равен 20+25+25+16+16+20+40=162 см
Я сам в интернете ищу