Дана фигура p. а) отразить фигуру р относительно оси ох и обозначьте d.
b) отразите фигуру p относительно начала координат и обозначьте е.

Дана фигура p. а) отразить фигуру р относительно оси ох и обозначьте d. b) отразите фигуру p относит

👇

Увидеть ответ

Ответ:

pistolenter

22.08.2022

А). Отразить фигуру р отноч

4,4(4 оценок)

Ответ:

Пушок771

22.08.2022

САМ НЕЗНАЮ СОР СДЕЛАТЬ

Объяснение:

4,4(34 оценок)

Открыть все ответы

Ответ:

zoology1g

22.08.2022

Глава 3. Параллельные прямые

3.2. Признаки параллельных прямых
Cледующая теорема дает достаточные условия параллельности (т. е. условия, выполнение которых гарантирует параллельность) двух прямых. Иначе такую теорему можно назвать признаком параллельности прямых:

Теорема 3.1.
Если внутренние накрест лежащие углы равны, то прямые параллельны.

Доказательство
До ознакомления с доказательством теоремы 3.1 необходимо изучить раздел 4.1 и теоремы 4.1 и 4.2 главы 4. Докажем теорему так называемым методом от противного: предположим, что условие теоремы выполнено, а именно: прямые AB и CD образуют с секущей AC равные внутренние накрестлежащие углы, но вопреки утверждению теоремы прямая AB не паралельна прямой CD и, следовательно, они пересекаются в точке O, которая лежит в одной из полуплоскостей от прямой AC.

1
Рисунок 3.2.1.
К теореме 3.1.

Отложим от луча АC треугольник AO1C, равный COА, так, что вершина O1 лежит в другой, нежели точка O, полуплоскости. Из равенства этих треугольников следует, что , ; по условию: и тогда точки O, C, лежат на одной прямой, и, аналогично, из равенства по условию углов OCA и смежного к BAC следует, что точки O1, A, O лежат также на одной прямой. Отсюда следует, что через две различные точки O и O1 плоскости проходят две различные прямые AB и CD. Это противоречит аксиоме 1.2. Полученное противоречие доказывает теорему.

На основании теоремы 3.1 можно легко доказать еще несколько признаков параллельности.

Если соответственные углы равны, то прямые параллельны.

Если сумма внутренних односторонних углов равна 180°, то прямые параллельны.

Из данного утверждения вытекает

Следствие 3.1.
Две прямые, перпендикулярные третьей, параллельны.

4,7(61 оценок)

Ответ:

bohdan4ever

22.08.2022

Объяснение:

а) Если две хорды в окружности пересекаются, то произведение отрезков одной хорды, равно произведению отрезков другой.

То есть: АО*СО=ВО*DO

x*(x+10)=(x+2)(x+4)

x²+10x=x²+4x+2x+8

x²–x²+10x–4x–2x=8

4x=8

x=2

ответ: 2.

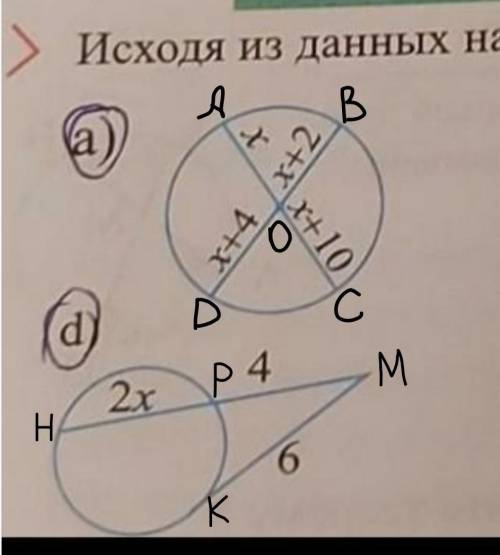
b) Если из одной точки к окружности проведены две секущие, то произведение одной секущей, на её внешнюю часть, равно произведению другой секущей на её внешнюю часть.

То есть: RG*RW=RL*RN

(RW+WG)*RW=(RN+NL)*RN

(4+8)*4=(3+x)*3

48=9+3x

3x=39

x=13

ответ: 13

с) Если из одной точки к окружности проведены две секущие, то произведение одной секущей, на её внешнюю часть, равно произведению другой секущей на её внешнюю часть.

То есть:

AD*AC=AM*AB

(AC+CD)*AC=(AB+BM)*AB

(x+x–2)*x=(4+x+1)*4

2*(x–1)*x=(5+x)*4

x²–x=10+2x

x²–x–2x–10=0

x²–3x–10=0

Д=(–3)²–4*1*(–10)=9+40=49

$x1 = \frac{3 + \sqrt{49} }{2 \times 1} = \frac{3 + 7}{2} = 5 \\ x2 = \frac{3 - \sqrt{49} }{2 \times 1} = \frac{3 - 7}{2} = - 2$

Так как длина задаётся положительным числом, что х=5.

ответ: 5

d) Если из одной точки к окружности проведена касательная и секущая, то квадрат отрезка касательной будет равен произведению отрезка секущей на её внешнюю часть.

То есть:

МК²=МН*МР

МК²=(МР+РН)*МР

6²=(2х+4)*4

36=8х+16

8х=20

х=2,5

ответ: 2,5

е) Если из одной точки к окружности проведена касательная и секущая, то квадрат отрезка касательной будет равен произведению отрезка секущей на её внешнюю часть.

То есть:

АМ²=АЕ*АО

АМ²=(АО+ОЕ)*АО

16²=(х+х+16)*х

256=(2х+16)*х

2х²+16х=256

х²+8х–128=0

Д=8²–4*1*(–128)=64+512=576

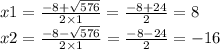
$x1 = \frac{ - 8 + \sqrt{576} }{2 \times 1} = \frac{ - 8 + 24}{2} = 8 \\ x2 = \frac{ - 8 - \sqrt{576} }{2 \times 1} = \frac{ - 8 - 24}{2} = - 16$

Так как длина не может быть отрицательной, то х=8.

ответ: 8.

f) Если из одной точки к окружности проведены две секущие, то произведение одной секущей, на её внешнюю часть, равно произведению другой секущей на её внешнюю часть.

То есть:

ON*OS=OA*OK

(OS+SN)*OS=(OK+KA)*OK

(x+5+x)*x=(5+5+x)*5

(2x+5)*x=(10+x)*5

2x²+5x=50+5x

2x²+5x–5x=50

x²=25

Совокупность:

х=√5

х=–√5

Так как длина – положительное число, то х=√5