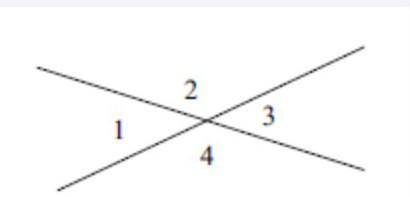
Решение, а) По условию Z2 + Z4 = 220°. Эти углы вертикальные, поэтому Z2 = Z4 = 110°.
Углы 1 и 2 смежные, поэтому Zl + Z2 = 180°, откуда Z1 = 180° -- 110° = 70°.
Углы 3 и 1 вертикальные, поэтому Z3 = Z1 = 70°.
б) Углы 1 и 3, а также 2 и 4 вертикальные, поэтому Z3 = Zl, Z4 = = Z2. Подставив эти выражения в данное равенство, получим:
3(2Z1) = 2Z2,
или
3Z1 =Z2.
Углы 1 и 2 смежные, поэтому Zl + Z2 = 180°. Из этих двух равенств находим Z1 и Z2: Z1 = 45°, Z2 = 135°.
Z3 = Z1, поэтому Z3 = 45°; Z4 = Z2, поэтому Z4 = 135°
в) По условию Z2 — Z1 = 30°. Эти углы смежные, следовательно, Zl + Z2 = 180°. Из этих двух равенств имеем: Z1 = 75°, Z2 = 105°.
Z3 = Z1, поэтому Z3 = 75°; Z4 = Z2, поэтому Z4 = 105°.
ответ, a) Zl = Z3 = 70°, Z2 = Z4 = 110°; б) Zl =Z3 = 45°, Z2 = = Z4 = 135°; в) Zl = Z3 = 75°, Z2 = Z4 = 105°.
Дано:
MABCD - правильная пирамида
MO⊥(ABCD)
MA = MB = MC = MD = 10
P(ABCD) = 24√2
-------------------------------------------------------------------------
Найти:
SO - ?
В правильном пирамиде в основании лежит квадрат ABCD, значит мы находим сторону основание квадрата:
AB = BC = CD = AD = P/4 = 24√2 / 4 = 6√2
Далее мы находим диагональ квадрата AC по такой формуле:
AC = AB√2 = 6√2 × √2 = 6×(√2)² = 6×2 = 12
Далее мы находим половину диагонали квадрата в правильной пирамиде:
AO = AC/2 = 12/2 = 6 ⇒ AO = OC = 6
И теперь находим высоту MO по теореме Пифагора:
AM² = AO² + MO² ⇒ MO = √AM² - AO²
MO = √10² - 6² = √100-36 = √64 = 8
ответ: MO = 8