x=-31/5 или -6.2
Объяснение:
1. Найдем уравнение прямой , на которой лежит вектор а (3;-5)
Коэффициент направления равен -5/3.
Тогда уравнение прямой: y= -5/3 *x
Вектор АВ коллинеарен вектору а, то есть лежит на прямой параллельной а
Тогда в уравнении прямой, на которой находится вектор АВ
y=ax+b коэффициент направления а также равен -5/3
Используем координаты точки А(-5;1) , чтобы найти b
1=-5/3*(-5)+b
25/3+b=1
b=1-25/3
b=-22/3
Найдем абсциссу точки пересечения найденной прямоу с прямой у=3
-5/3*x-22/3=3
-5/3*x= 3+22/3
-5/3*x=31/3
x=- 31/5
x= -6.2
Объяснение:
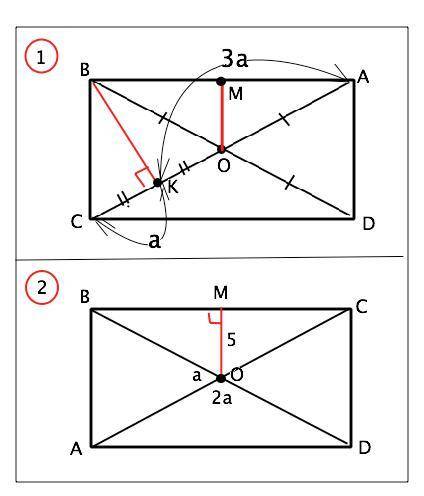
1)Обозначим данный прямоугольник АВСD. Отрезок ВК⊥АС. АК:КС=3:1. О - точка пересечения диагоналей. (см. рисунок приложения),
Диагонали прямоугольника равны и точкой пересечения делятся пополам. . АС=ВD=8, ВО=ОС=АО=ОD=4.
Диагональ АС содержит 3+1=4 части, тогда СК=1 часть=8:4=2 см,⇒ КО=4-2=2 см. ВК - высота треугольника ВОС (перпендикулярна отрезку СО) и делит его пополам. Следовательно, является его медианой, поэтому ∆ ВСО равнобедренный. ВС=ВО. Но ВО=СО ⇒ ∆ СВО - правильный, В ∆ ВОМ угол ОВМ=∠СВМ-СВО=90°-60°=30° Катет ОМ противолежит углу 30° и равен половине гипотенузы ВО. ⇒ ОМ=АЕ=2 см.
———————
2) Расстояние от точки до прямой равно длине проведенного к ней перпендикуляра. В прямоугольнике АВСD это отрезок ОМ.
Угол ВOD - развернутый и равен 180°. Сумма смежных углов ВОА и АОD равна 1+2=3 части. ⇒ угол ВОА=1 часть=180°:3=60°. По свойству диагоналей прямоугольника ВО=АО, поэтому углы при основании АВ равнобедренного ∆ ВОА равны (180°-60*):2=60°, из чего следует: в прямоугольном ∆ ВОМ угол ОВМ=угол АВМ-угол АВО=90°-60°=30°. Гипотенуза ВО в два раза больше катета, противолежащего углу 30° ⇒ ВО=10 см. ВО = половина диагонали. Диагональ ВD=2•10=20 см.
Треугольник АВС, АС =12 ВМ =высота, медиана, биссектриса на АС, АМ=СМ=6
точка О - центр вписанной окружности в треугольник АВС - пересечение биссектрис треугольника, ОМ = радиус вписанной окружности
точка О1 = центр окружности с радиусом =8, проводим перпендикуляры О1К и О1Н в точки касания, проводим О1С и О1А, треугольники АМО1=треугольнику О1СМ по двум катетам АМ=СМ, О1М общий, треугольники О1СК =треугольнику О1СМ по гипотенузе О1С и катету О1К=О1М =радиусу, треугольник О1НА=треугольнику О1МА по катету и гипотенузе (аналогично), угол О1СМ=углу О1СК , угол СО1К=углу СО1М значит СО1 - биссектриса, СО - тоже биссектриса (см.выше). Биссектрисы внутреннего угла и смежного с ним внешнего угла перпендикулярны, т.е угол ОСО1 =90 град. Треугольник ОСО1 - прямоугольный.
ОМ / СМ = СМ / О1М, ОМ / 6 = 6 / 8
36 = ОМ х 8, ОМ = 4,5