ответ:8 см
Объяснение:
Пусть дана окружность с центром в т.О. Проведем прямую, которая пересечет окружность в т. А и т.В, т.о. АВ - хорда, АВ = 12 см. Т.к. т.А и В лежат на окружности, то ОА = ОВ = 10 см - это радиусы окружности. Получим треугольник АОВ - равнобедренный, АВ - основание. Проведем ОК ⊥ АВ, ОК - расстояние от центра до хорды. Значит ОК - медиана , АК = ВК = 12 : 2 = 6 см. Рассмотрим треугольник ОКА - прямоугольный и найдем ОК используя теорему Пифагора.
ОК² = ОА² - АК² , ОК² = 100 - 36 = 64 см², ОК = корень из 64 = 8 см
ответ: 8см
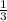BK=
. Значит, DK=2NK=2. Считаем площадь равнобедренного ADC=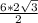
=6. Получаем, наконец, площадь полной поверхности: 3+3*6=21 (площадь основания плюс площади трех боковых граней).
. И наконец, V=9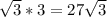
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов всех его измерений (то есть ширины, длины и высоты).
22² = (2х)² + (6х)² + (9х)²
484 = 4х² + 36х² + 81х²
484 = 121х²
х² = 484 : 121
х² = 4
х =2 - одна часть.
2 * х = 2 * 2 = 4
6 * х = 6 * 2 = 12
9 * х = 9 * 2 = 18.
Ребра равны 4 дм, 12 дм, 18 дм.