1) 60/13
2) АD=13
3) 60√3
4) 120/13
Объяснение:
ABCD-ромб⇒АС⊥ВD, АО=0,5АС, DО=0,5ВD
АО=0,5АС=0,5·10=5
DО=0,5ВD=0,5·24=12
АС⊥ВD, по теореме Пифагора АD²=АО²+DО²=5²+12²=25+144=169⇒АD=13
2) АВ=ВС=СD=АD=13-сторона ромба
3) Площадь орт.проекции фигуры на плоскость равна произведению площади данной фигуры на косинус угла между плоскостью и данной фигурой.
Площадь ромба по готовой формуле: S=0,5AC·BD=0,5·10·24=120
Площадь орт проекции: s=S·cos((ABCD)∧α)=120·cos30°=120·√3/2=60√3
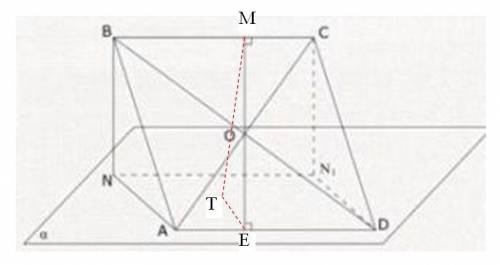
4) Через точку О - пересечение диагоналей ромба проведём перпендикуляр к стороне ВС, OM⊥BC.
Но так как ВС║AD⇒ME⊥AD, ME⊥BC⇒ME-высота ромба.
Ещё одна формула для нахождения площади ромба
S=ME·AD⇒120=ME·AD=13ME⇒ME=120/13
1) Опустим из точки М перпедикуляр МТ на плоскость α.
МТ⊥α, Е∈α⇒отрезок TE есть орт.проекция отрезка МЕ на плоскости α.
АD⊥МЕ⇒АD⊥ТЕ(теорема о трёх перпендикулярах)
Значить, ∠МЕT=(АВСD∧α)=30°
МТ⊥α, ЕТ∈α⇒МТ⊥ ЕТ⇒∠МТЕ=90°
∠МТЕ=90°,∠МЕT=30°⇒MT=0,5ME=0,5 ·120/13=60/13
Растояние между ВD и пл.α и есть отрезок МТ=60/13
Р.S. Все 4 пункта вычислены. Соответствие это выбор подходящего варианта ответа
1-В
2-А
3-Б
4-Д
ВС = 3√21 см.
Объяснение:
Пусть основание перпендикуляра, опущенного на плоскость α - точка Н.
AH=9 см,<ABH=45°,<ACH=60°,<BHC=150°.
Заметим, что Cos150° = Cos(180 - 30) = -Cos30° = - √3/2.
В прямоугольном треугольнике АВН острые углы равны по 45°, треугольник равнобедренный и ВН=АН= 9см.
В прямоугольном треугольнике АСН тангенс угла С равен
Tg60 = √3 = AH/CH => CH = 9/√3 = 3√3 см.
В треугольнике ВНС по теореме косинусов:
BC²=BH²+CH²-2*BН*CH*cos150 = 81+27 - 2*9*3√3*(-√3/2) или
ВС² = 108+81 =189
BC = √189 = 3√21 см.