1) радиус вписанной окружности равен 5
радиус описанной окружности равен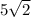 
2) 4 - стороны у квадрата
Объяснение:
1) радиус вписанной окружности равен 5 см
2) это квадрат. Так как, если вписать в него окружность, то радиус этой окружности равен половине стороны квадрата.
То есть 10см (длина стороны квадрата) :2=5 см (длина радиуса вписанной окружности)
Ну у квадрата 4 стороны.
Если же это радиус описанной окружности, то он равен половине диагонали квадрата. По теореме Пифагора диагональ квадрата равна
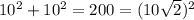
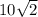- диагональ данного квадрата
Теперь его половина равна
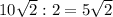
такого треугольника не существует
или 60 см^2.
Объяснение:
Треугольника с заданными сторонами не существует.
13 см > 10см + 13мм, не выполнено неравенство для сторон треугольника.
Если в условии опечатка, длины стороны треугольника 13 см, 13 см, 10 см, то площадь может быть найдена по формуле Герона:
S = √p•(p-a)•(p-b)•(p-c).
p = (10+13+13):2 = 18 (см),
S = √18•(18-13)•(18-13)•(18-10) = √(18•5^2•8) = √(9•5^2•16) = 3•5•4 = 60 (см^2)
Ещё одним может быть нахождение по формуле
S = 1/2•a•h, где а = 10 см, а длина высоты найдена по теореме Пифагора из прямоугольного треугольника, образованного боковой стороной, высотой, проведённой к основанию, и половиной основания, h = 12 см.
(S = 1/2•10•12 = 60 (см^2) ).
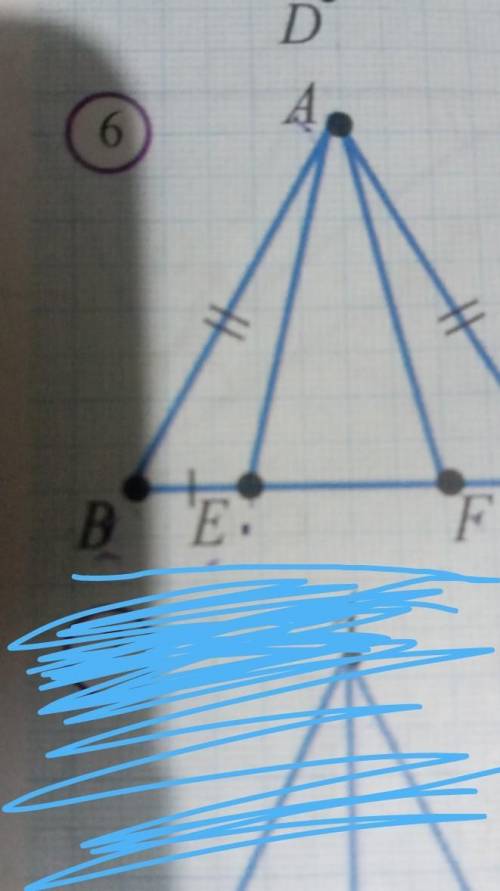
a) так как DA Общая ,а AB =AC ,BE =CF, то DABE =DACF. .б) треугольнк ABC Равнобедреный . угол В равен углу C. сладовательно треугольникABE равен треугольнику ACF. значчит AE =AF. в) не понятен вопрос или не вижу весь рисунок.