1) радиус вписанной окружности равен 5
радиус описанной окружности равен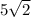 
2) 4 - стороны у квадрата
Объяснение:
1) радиус вписанной окружности равен 5 см
2) это квадрат. Так как, если вписать в него окружность, то радиус этой окружности равен половине стороны квадрата.
То есть 10см (длина стороны квадрата) :2=5 см (длина радиуса вписанной окружности)
Ну у квадрата 4 стороны.
Если же это радиус описанной окружности, то он равен половине диагонали квадрата. По теореме Пифагора диагональ квадрата равна
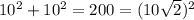
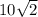- диагональ данного квадрата
Теперь его половина равна
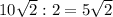
↑АС = ↑р = ↑а + ↑b
↑DB = ↑q = ↑a - ↑b
Чтобы найти угол между векторами p и q, построим вектор, равный вектору q, с началом в точке А.
∠ЕАС - искомый.
Из ΔABD найдем длину вектора q по теореме косинусов:
|↑q|² = AB² + AD² - 2·AB·AD·cos60° = 25 + 64 - 2·5·8·1/2 = 89 - 40 = 49
|↑q| = 7
Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°, значит ∠АВС = 120°.
Из ΔABС найдем длину вектора р по теореме косинусов:
|↑p|² = AB² + BC² - 2·AB·BC·cos120° = 25 + 64 + 2·5·8·1/2 = 89 + 40 = 129
|↑p| = √129
Из ΔЕАС по теореме косинусов:
cos α = (AE² + AC² - EC²) / (2 · AE · AC)
cos α = (49 + 129 - 256) / (2 · 7 · √129) = - 78 / (14√129) = - 39√129 / 903
cos α = - 13√129/301