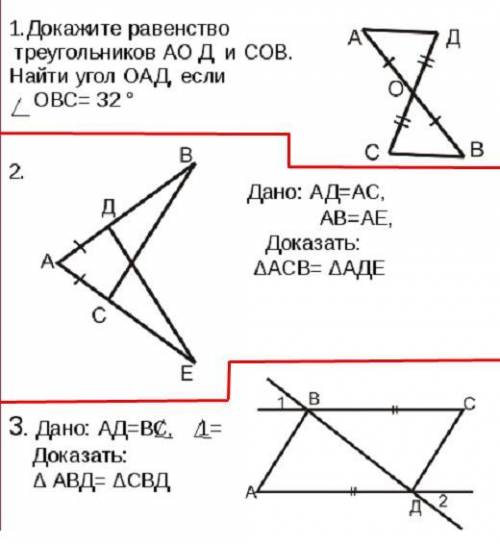
1.
Рассмотрим треугольники АОД и СОВ:
1) АО=ОВ (по условию)
2)ОД=ОС (по условию)
3) угол АОД=СОВ (так как это вертикальные углы)
Значит, треугольник АОД= треугольнику ВОС по первому признаку равенства треугольников.
Мы доказали равенство треугольников, а в равных треугольниках все элементы также равны (перефразируй, не знаю как написать).
Значит угол ОАД= углу ОВС.
Поэтому- угол ОАД= 32°
PS: я доказывала равенство углов с трёх равных элементов.
PS2: решу и остальное скину в комментарии.
1) По формуле расстояния между 2-мя точками найдем длину стороны АВ:
АВ=sqrt((2+6)^2+(4-1)^2)=sqrt(64+9)=sqrt(73).
2) Аналогично: ВС=sqrt((2-2)^2+(-2-4)^2)=sqrt(0+36)=sqrt(36)=6;
АС=sqrt((2+6)^2+(-2-1)^2)=sqrt(64+9)=sqrt(73).
3) Итак, стороны АВ и АС равны, значит тр-к АВС - равнобедренный, ч.т.д.
4) Найдем площадь тр-ка АВС по формуле: половина произведения стороны на высоту, проведенную к этой стороне. Сначала опустим из т. А на ВС высоту АД. Высота АД - так же является медианой и биссектрисой (св-во равнобедр-го тр-ка). Координаты точки Д найдем по формулам координат середины отрезка ВС:
х=(2+2)/2=2; у=(4-2)/2=1. Тогда длина ВД равна:
sqrt((2+6)^2+(1-1)^2)=sqrt(64+0)=sqrt(64)=8.
Площадь тр-ка АВС равна: 1/2*ВС*ВД=1/2*6*8=24 (квадр. см)
1.т.АОД=т.ОСВ(по признаку о двух сторонах и углу между ними)
угол ОВС=углуОАД=32(по равенству треугольников)
2. т. АСВ=т.АДЕ(по признаку о общем угле А и АД=АС, АВ=АЕ)
3.т.АВД=т.СВД(по признаку о ВС=АД и у. 1=у.2 как соответственные углы
Совет тебе) Лучше выучи признаки, в будущем они часто будут встречаться)